题目内容
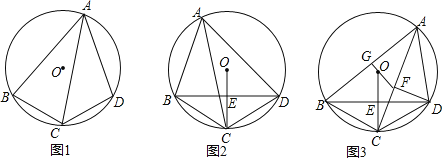
【题目】四边形ABCD内接于⊙O,AC为其中一条对角线,且S△ABC:S△ADC=AB:AD.
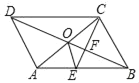
(1)如图1,求证:BC=CD;
(2)如图2:连接OC,交对角线BD于点E,若∠BAD=60°,求证:OE=EC;
(3)如图3,在(2)的条件下,过点D作DF⊥AC于点F,连接FO并延长FO,交AB边于点G,若FG⊥AB,OC=![]() ,求△OFC的面积.
,求△OFC的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)首先利用已知得出CL=CK,再结合全等三角形的判定方法得出△CKB≌△CLD(AAS),进而得出答案;
(2)首先得出△OBC是等边三角形,进而得出答案;
(3)利用已知首先得出△AMD是等边三角形,进而得出BG,EF的长,再利用S△OEF=![]() OFEF进而得出答案.
OFEF进而得出答案.
(1)证明:过C作CK⊥AB于点K,过C作CL⊥AD于点L,
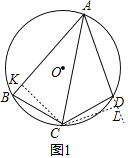
∴S△ABC=![]() ABCK,S△ADC=
ABCK,S△ADC=![]() ADCL,
ADCL,
∵S△ABC:S△ADC=AB:AD.
∴CL=CK,
∵∠B+∠ADC=180°,∠CDL+∠ADC=180°,
∴∠B=∠CDL,
∵∠CKB=∠L=90°,
在△CKB和△CLD中
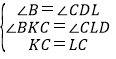 ,
,
∴△CKB≌△CLD(AAS),
∴BC=CD.
(2)证明:如图2,连接OB、OD,
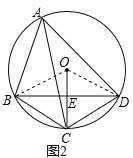
∵BC=CD,
∴∠BOC=∠DOC
∵OB=OD,
∴OE⊥BD,
∵∠BAD=60°,
∴∠BOC=∠DOC=60°,
∴△OBC是等边三角形,
∴OB=BC,
∴OE=EC;
(3)如图3,延长DF交AB于点M,连接OB,
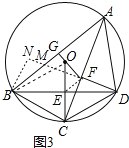
∵∠BAD=60°,
∴∠BAC=∠CAD=30°,
∵AF⊥DF,
∴∠AFM=∠AFD=90°,
∴∠AMD=∠ADM=60°,
∴△AMD是等边三角形,
设MG=a,则MF=2a,AM=AD=MD=4a,GF=![]() a,
a,
∴AG=BG=3a,∴BM=2a
∵E、F分别是BD、MD中点,∴EF=a,EF∥AB
过B作BN⊥MD,则MN=a,BN=![]() a,∴DN=5a,
a,∴DN=5a,
∵BD=![]() OC,
OC,
∴BD=3![]()
在Rt△BND中,(![]() a)2+(5a)2=/span>(3
a)2+(5a)2=/span>(3![]() )2
)2
解得a=![]() ,
,
∴BG=![]() ,EF=
,EF=![]() ,
,
在Rt△OGB中,OG=![]() ,
,
∴OF=![]() ,
,
∵EF∥AB,
∴∠EFO=∠AGF=90°
∴S△OEF=![]() OFEF=
OFEF=![]() ×
×![]() ×
×![]() =
=![]()
∵OE=EC,
∴S△OFC=2S△OEF=![]() .
.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案