Question

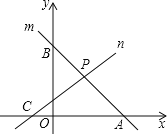
【题目】如图，直线分别与轴，轴交于两点，与直线交于点.

（1）点的坐标为__________，点的坐标为__________

（2）在线段上有一点，过点作轴的平行线交直线于点，设点的横坐标为，当为何值时，四边形是平行四边形.

Answer 1

【答案】（1）（8，0） , （0，4） ；（2）当m为时，四边形OBEF是平行四边形．

【解析】

（1）由点C的坐标利用待定系数法即可求出直线的解析式，再分别令直线的解析式中x=0、y=0求出对应的y、x值，即可得出点A、B的坐标；

（2）由点C的坐标利用待定系数法即可求出直线的解析式，结合点E的横坐标即可得出点E、F的坐标，再根据平行四边形的性质即可得出关于m的一元一次方程，解方程即可得出结论；

解：（1）将点C(4,2)代入y= x+b中，

得：2=2+b，解得：b=4，

∴直线为y=x+4.

令y=x+4中x=0，则y=4，

∴B(0,4)；

令y=x+4中y=0，则x=8，

∴A(8,0).

故答案为：（8，0）（0，4）

（2）将C（4，2）分别代入y=－x+b， y=kx－6，得b=4，k=2.

∴直线l1的解析式为y=－x+4，直线l2的解析式为y=2x－6．

∵点E的横坐标为m，

∴点E的坐标为（m，－m+4），点F的坐标为（m，2m－6）.

∴EF=－m+4－（2m－6）=－m+10．

∵四边形OBEF是平行四边形，

∴EF=OB，即－m+10=4.

解得m=.

∴当m为时，四边形OBEF是平行四边形．