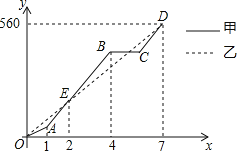
题目内容
【题目】一个二元一次方程ax+by=c(a,b,c,为常数,且A,B均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标极点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,既二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,即2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).
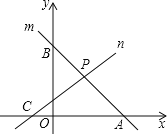
(1)如图,3x+3y=12,的图象为直线m,其与x轴交点A的坐标为____,其与y轴交点B的坐标为___;
(2)如图,ax+by=-5的图象为直线n,其与x轴交于C(-![]() ,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值.
,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值.
【答案】(1)(4,0);(0,4);(2)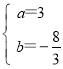 ;
;
【解析】
(1)分别令3x+3y=12中y=0、x=0求出与之相对应的x、y值,由此即可得出点A、B的坐标;
(2)将x=1代入3x+3y=12中求出y值,即可得出点P的坐标,由点C、P的坐标利用待定系数法即可求出a、b的值.
(1)令3x+3y=12中y=0,则3x=12,解得:x=4,
∴A(4,0);
令3x+3y=12中x=0,则3y=12,解得:y=4,
∴B(0,4).
故答案为:(4,0);(0,4).
(2)令3x+3y=12中x=1,则3+3y=12,解得:y=3,
∴P(1,3).
将C(-![]() ,0)、P(1,3)代入ax+by=-5中,
,0)、P(1,3)代入ax+by=-5中,
得: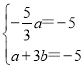 ,解得:
,解得: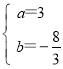 .
.

【题目】某商场试销一种成本为50元/件的![]() 恤.经试销发现,销售量
恤.经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数关系,试销数据如下表:
(元/件)符合一次函数关系,试销数据如下表:
售价(元/件) | …… | 55 | 60 | 70 | …… |
销量(件) | …… | 75 | 70 | 60 | …… |
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价![]() 之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?