题目内容
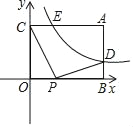
【题目】如图所示,已知矩形ABOC中,AC=4,双曲线y=![]() 与矩形两边AB、AC分别交于D、E,E为AC边中点.
与矩形两边AB、AC分别交于D、E,E为AC边中点.
(1)求点E的坐标;
(2)点P是线段OB上的一个动点,是否存在点P,使∠DPC=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
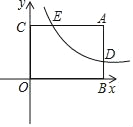
【答案】(1)点E的坐标为(2,3);(2)不存在点P,使∠DPC=90°
【解析】分析:(1)根据矩形的性质求出点E的横坐标为2,代入反比例函数解析式计算,求出点E的坐标;
(2)设点P的坐标为(a,0),证明△COP∽△PBD,根据相似三角形的性质列出方程,根据一元二次方程根的判别式解答.
详解:(1)矩形ABOC中,AC=4,E为AC边中点,
∴CE=2,即点E的横坐标为2,
∵点E在双曲线y=![]() 上,
上,
∴y=![]() =3,
=3,
∴点E的坐标为(2,3);
(2)不存在点P,使∠DPC=90°,
理由如下:设点P的坐标为(a,0),
则OP=a,PB=4﹣a,
由题意可知,点D的横坐标为4,
则纵坐标为:y=![]() =
=![]() ,即BD=
,即BD=![]() ,
,
∵∠COP=∠CPD=∠PBD=90°,
∴△COP∽△PBD,
∴![]() =
=![]() ,即
,即![]() ,
,
整理得,a2﹣4a+![]() =0,
=0,
△=16﹣18<0,
∴方程无实根,
∴不存在点P,使∠DPC=90°.

练习册系列答案
相关题目