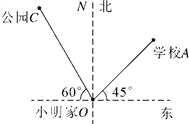
题目内容
【题目】在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°.
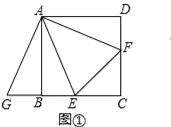
(1)将△ADF绕着点A顺时针旋转90°，得到△ABG(如图①)，求证：△AEG≌△AEF；
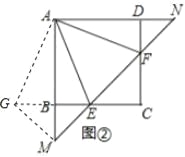
(2)若直线EF与AB，AD的延长线分别交于点M，N(如图②)，求证：EF2=ME2+NF2；
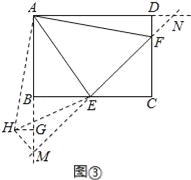
(3)将正方形改为长与宽不相等的矩形，若其余条件不变(如图③)，请你直接写出线段EF，BE，DF之间的数量关系.
【答案】（1）证明见解析；（2）证明见解析；（3）EF2=2BE2+2DF2.
【解析】试题分析：（1）根据旋转的性质可知AF=AG，∠EAF=∠GAE=45°，故可证△AEG≌△AEF；
（2）将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．由（1）知△AEG≌△AEF，则EG=EF．再由△BME、△DNF、△CEF均为等腰直角三角形，得出CE=CF，BE=BM，NF=
DF，然后证明∠GME=90°，MG=NF，利用勾股定理得出EG2=ME2+MG2，等量代换即可证明EF2=ME2+NF2；
（3）将△ADF绕着点A顺时针旋转90°，得到△ABG，根据旋转的性质可以得到△ADF≌△ABG，则DF=BG，再证明△AEG≌△AEF，得出EG=EF，由EG=BG+BE，等量代换得到EF=BE+DF．
试题解析：（1）∵△ADF绕着点A顺时针旋转90°，得到△ABG，
∴AF=AG，∠FAG=90°，
∵∠EAF=45°，
∴∠GAE=45°，
在△AGE与△AFE中，
，
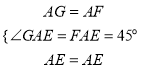∴△AGE≌△AFE（SAS）；
（2）设正方形ABCD的边长为a．
将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．
则△ADF≌△ABG，DF=BG．
由（1）知△AEG≌△AEF，
∴EG=EF．
∵∠CEF=45°，
∴△BME、△DNF、△CEF均为等腰直角三角形，
∴CE=CF，BE=BM，NF=
DF，
∴a﹣BE=a﹣DF，
∴BE=DF，
∴BE=BM=DF=BG，
∴∠BMG=45°，
∴∠GME=45°+45°=90°，
∴EG2=ME2+MG2，
∵EG=EF，MG=
BM=
DF=NF，
∴EF2=ME2+NF2；
（3）EF2=2BE2+2DF2．
如图所示，延长EF交AB延长线于M点，交AD延长线于N点，
将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．
由（1）知△AEH≌△AEF，
则由勾股定理有（GH+BE）2+BG2=EH2，
即（GH+BE）2+（BM﹣GM）2=EH2
又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）2+（BE﹣GH）2=EF2，
即2（DF2+BE2）=EF2
