题目内容
【题目】如图,在矩形ABCD中,AB=3,BC=4,点M是BC的中点,点P从点M出发沿MB以每秒1个单位的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;同时点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作正方形PQEF,使它与矩形ABCD在BC的同侧,点P,Q同时出发,当点P返回点M时,则两点停止运动,设点P,Q运动的时间是t秒(t>0).
(1)当点P运动到BM的中点时,t= ;
(2)设正方形PQEF与矩形ABCD重叠部分的面积为S,直接写出S与t之间的函数关系式及t的取值范围;
(3)连结AC,当正方形PQEF与△ADC重叠部分为三角形时,求t的取值范围.
【答案】(1)1或3;(2)①S=4t2;②S=6t;③S=﹣3t+18;(3)![]() <t≤
<t≤![]() 或t=2
或t=2
【解析】分析:(1)求出BM=![]() BC=2,当点P第一次运动到BM的中点时,PM=
BC=2,当点P第一次运动到BM的中点时,PM=![]() BM=1,得出t=1;当点P第二次运动到BM的中点时,运动的路程=3,得出t=3即可;
BM=1,得出t=1;当点P第二次运动到BM的中点时,运动的路程=3,得出t=3即可;
(2)分为三种情况:①当0<t≤1.5时,PQ=2t,由正方形面积公式即可得出答案;
②当1.5<t≤2时得出PQ=2t,AB=3,由矩形面积即可得出答案;
③当2<t≤4时,求出PC=6-t,AB=3,由矩形面积即可得出答案;
(3)当点E在AC上时,得出△CEQ∽△CAB,得出对应边成比例,即可得出t的值;当F在AC上时,△CPF∽△CBA,得出对应边成比例,即可得出t的值;当点F在EA的延长线上时,点E在CD的延长线上,此时t=2;即可得出答案.
详解:(1)∵BC=4,点M是BC的中点,
∴BM=![]() BC=2,
BC=2,
当点P第一次运动到BM的中点时,PM=![]() BM=1,
BM=1,
∴t=1;
当点P第二次运动到BM的中点时,运动的路程=2+1=3,
∴t=3;
故答案为:1或3;
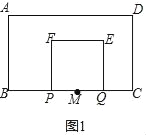
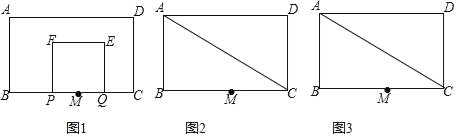
(2)分为三种情况:
①如图1,当0<t≤1.5时,
∵PQ=2t,
∴S=(2t)2,
∴S=4t2;
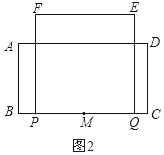
②如图2,
当1.5<t≤2时,
∵PQ=2t,AB=3,
∴S=6t;
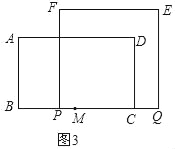
③如图3,
当2<t≤4时,
∵PC=6﹣t,AB=3,
∴S=﹣3t+18;
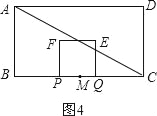
(3)如图4,
当点E在AC上时,
∵△CEQ∽△CAB,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
当F在AC上时,
∵△CPF∽△CBA,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ;当点F在EA的延长线上时,点E在CD的延长线上,此时t=2;
;当点F在EA的延长线上时,点E在CD的延长线上,此时t=2;
∴t的取值范围是![]() <t≤
<t≤![]() 或t=2.
或t=2.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案