题目内容
【题目】(1)问题背景:
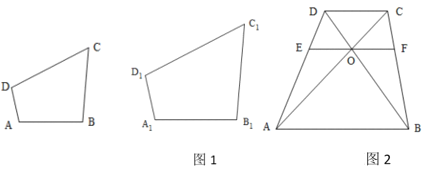
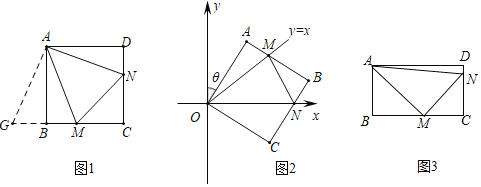
如图1,在正方形ABCD中,点M,N分别在边BC,CD上,连接MN,且∠MAN=45°,将△ADN绕点A顺时针旋转90°,得到△ABG,可证△AMG≌△AMN,易得线段MN、BM、DN之间的数量关系为: (直接填写);
(2)实践应用:
在平面直角坐标系中,边长为5的正方形OABC的两顶点分别在y轴、x轴的正半轴上,O在原点.现将正方形OABC绕点O按顺时针方向旋转,旋转角为θ,当点A第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.如图2,设△MBN的周长为P,在旋转正方形OABC的过程中,P值是否有变化?请证明你的结论;
(3)拓展研究:
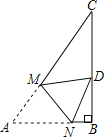
如图3,将正方形改为长与宽不相等的矩形,且∠MAN=∠CMN=45°,请你直接写出线段MN、BM、DN之间的数量关系.
【答案】(1)MN=BM+DN;(2)在旋转正方形OABC的过程中,P值不变;(3)MN2=2BM2+2DN2 ,理由见解析.
【解析】
(1)由旋转的性质可得出DN=BG,由全等的性质可得出MG=MN,结合MG=BM+BG即可得出MN=BM+DN;
(2)将△AOM绕点O顺时针旋转90°,得到△COE,易证△MON≌△EON(SAS),利用全等三角形的性质可得出MN=EN=CN+AM,再利用三角形的周长公式结合正方形的边长,即可求出S的值;
(3)将△ABM绕点O逆时针旋转90°,得到△AB′M′,则△AMN≌△AM′N,利用全等三角形的性质可得出M′N=MN,由∠C=90°,∠CMN=45°可得出CM=CN,设BM=a,DN=b,CM=c,则AD=a+c,CD=b+c,进而可得出M′F=a﹣b,NF=b+a,在Rt△M′FN中,利用勾股定理可求出M′N2=2a2+2b2,进而可得出MN2=2BM2+2DN2.
解:(1)由旋转,可知:DN=BG.
∵△AMG≌△AMN,
∴MG=MN.
∵MG=BM+BG=BM+DN,
∴MN=BM+DN.
故答案为:MN=BM+DN.
(2)在旋转正方形OABC的过程中,P值不变.
证明:在图2中,将△AOM绕点O顺时针旋转90°,得到△COE.
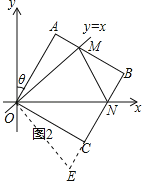
由旋转,可知:OM=OE,AM=CE,∠AOM=∠COE,∠MOE=90°.
∵直线OM的解析式为y=x,
∴∠MON=45°.
∵∠MOE=90°,
∴∠EON=45°.
在△MON和△EON中,
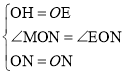 ,
,
∴△MON≌△EON(SAS),
∴MN=EN=CN+AM.
∴S=BM+BN+MN=BM+AM+BN+CN=2AB=10,
∴在旋转正方形OABC的过程中,P值不变.
(3)MN2=2BM2+2DN2.理由如下:
在图3中,将△ABM绕点O逆时针旋转90°,得到△AB′M′.
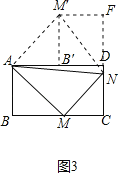
由(2)可知△AMN≌△AM′N,
∴M′N=MN.
∵∠C=90°,∠CMN=45°,
∴CM=CN.
设BM=a,DN=b,CM=c,则AD=a+c,CD=b+c,
∴M′F=AD﹣AB′=AD﹣AB=a+c﹣(b+c)=a﹣b,
NF=DN+DF=DN+B′M′=DN+BM=b+a.
在Rt△M′FN中,M′N2=M′F2+NF2=(a﹣b)2+(a+b)2=2a2+2b2,
∴MN2=2BM2+2DN2.

 名校课堂系列答案
名校课堂系列答案