题目内容
【题目】在⊙O中，
的度数为120°，点P为弦AB上的一点，连结OP并延长交⊙O于点C，连结OB，AC．
（1）若P为AB中点，且PC＝1，求圆的半径．
（2）若BP：BA＝1：3，请求出tan∠OPA．
【答案】（1）OC＝2；（2）
【解析】
（1）根据垂径定理，可得OC垂直平分AB，再由正弦定理可得圆的半径．（2）过点O作OD⊥AB于点D，根据勾股定理和正切公式，可得tan∠OPA．
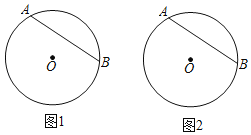
解：（1）如图1，
∵P是AB的中点，
的度数为120°，
∴OC⊥AB，
∴∠POB＝60°，∠OBP＝30°，
∴
，
∴OP＝PC＝1，
则OC＝2；
（2）如图2，
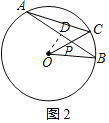
过点O作OD⊥AB于点D，
由（1）知∠B＝30°，AD＝BD，
∴ 
，
设OD＝x，则BD＝3x，
∵BP：BA＝1：3，
∴PD＝x，
∴tan∠DPO＝．
练习册系列答案
相关题目
