题目内容
【题目】根据相似多边形的定义，我们把四个角分别相等，四条边成比例的两个凸四边形叫做相似四边形．相似四边形对应边的比叫做相似比．
（1）某同学在探究相似四边形的判定时，得到如下三个命题，请判断它们是否正确（直接在横线上填写“真”或“假”）．
①条边成比例的两个凸四边形相似；（ 命题）
②三个角分别相等的两个凸四边形相似；（ 命题）
③两个大小不同的正方形相似．（ 命题）
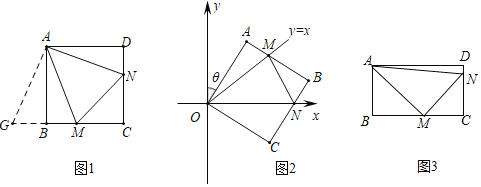
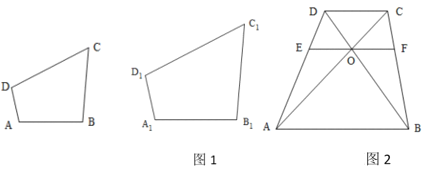
（2）如图1，在四边形ABCD和四边形A1B1C1D1中，∠ABC＝∠A1B1C1，∠BCD＝∠B1C1D1，
，求证：四边形ABCD与四边形A1B1C1D1相似．
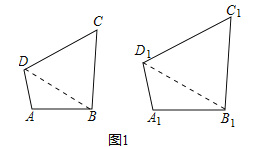
（3）如图2，四边形ABCD中，AB∥CD，AC与BD相交于点O，过点O作EF∥AB分别交AD，BC于点E，F．记四边形ABFE的面积为S1，四边形EFDE的面积为S2，若四边形ABFE与四边形EFCD相似，求
的值．
【答案】（1）①假，②假，③真；（2）见解析 ；（3）
【解析】
（1）根据相似多边形的定义即可判断．
（2）根据相似多边形的定义证明四边成比例，四个角相等即可．
（3）四边形ABFE与四边形EFCD相似，证明相似比是1即可解决问题，即证明DE=AE即可．
解（1）①四条边成比例的两个凸四边形相似，是假命题，角不一定相等．
②三个角分别相等的两个凸四边形相似，是假命题，边不一定成比例．
③两个大小不同的正方形相似．是真命题．
故答案为假，假，真．
（2）证明：分别连接BD，B1D1
，且
，
，
，
，
，
，
，
，
，
，
，
，
，，
，
四边形ABCD与四边形A1B1C1D1相似.
（3）如图2中，
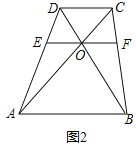
∵四边形ABFG与四边形EFCD相似
，
，
，
，
，
，
，
，
，
，
，即AE=DE
，
练习册系列答案
相关题目
