题目内容
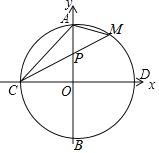
【题目】如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)求证:OP∥BC;
(2)过点C作⊙O的切线CD,交AP的延长线于点D.如果∠D=90°,DP=1,求⊙O的直径.
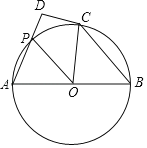
【答案】(1)见解析;(2)⊙O的直径AB=4.
【解析】
(1)由题意可知![]() ,根据同弧所对的圆心角相等得到∠AOP=
,根据同弧所对的圆心角相等得到∠AOP=![]() ∠AOC,再根据同弧所对的圆心角和圆周角的关系得出∠ABC=
∠AOC,再根据同弧所对的圆心角和圆周角的关系得出∠ABC=![]() ∠AOC,利用同位角相等两直线平行,可得出PO与BC平行;
∠AOC,利用同位角相等两直线平行,可得出PO与BC平行;
(2)由CD为圆O的切线,利用切线的性质得到OC垂直于CD,又AD垂直于CD,利用平面内垂直于同一条直线的两直线平行得到OC与AD平行,根据两直线平行内错角相等得到∠APO=∠COP,由∠AOP=∠COP,等量代换可得出∠APO=∠AOP,再由OA=OP,利用等边对等角可得出一对角相等,等量代换可得出三角形AOP三内角相等,确定出三角形AOP为等边三角形,根据等边三角形的内角为60°得到∠AOP为60°,由OP平行于BC,利用两直线平行同位角相等可得出∠OBC=∠AOP=60°,再由OB=OC,得到三角形OBC为等边三角形,可得出∠COB为60°,利用平角的定义得到∠POC也为60°,再加上OP=OC,可得出三角形POC为等边三角形,得到内角∠OCP为60°,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,而PC等于圆的半径OP等于直径AB的一半,可得出PD为AB的四分之一,即AB=4PD=4.
(1)证明:∵A关于OP的对称点C恰好落在⊙O上.
∴![]()
∴∠AOP=∠COP,
∴∠AOP=![]() ∠AOC,
∠AOC,
又∵∠ABC=![]() ∠AOC,
∠AOC,
∴∠AOP=∠ABC,
∴PO∥BC;
(2)解:连接PC,
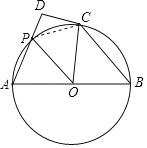
∵CD为圆O的切线,
∴OC⊥CD,又AD⊥CD,
∴OC∥AD,
∴∠APO=∠COP,
∵∠AOP=∠COP,
∴∠APO=∠AOP,
∴OA=AP,
∵OA=OP,
∴△APO为等边三角形,
∴∠AOP=60°,
又∵OP∥BC,
∴∠OBC=∠AOP=60°,又OC=OB,
∴△BCO为等边三角形,
∴∠COB=60°,
∴∠POC=180°﹣(∠AOP+∠COB)=60°,又OP=OC,
∴△POC也为等边三角形,
∴∠PCO=60°,PC=OP=OC,
又∵∠OCD=90°,
∴∠PCD=30°,
在Rt△PCD中,PD=![]() PC,
PC,
又∵PC=OP=![]() AB,
AB,
∴PD=![]() AB,
AB,
∴AB=4PD=4.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案