题目内容
【题目】（本题满分10分）在平面直角坐标系中，抛物线y=x
+5x+4的顶点为M，与x轴交于A、B两点与y轴交于C点。
（1）求点A、B、C的坐标；
（2）求抛物线y=x+5x+4关于坐标原点O对称的抛物线的函数表达式；
（3）设（2）中所求抛物线的顶点为
,与x轴交于
、
两点，与y轴交于
点，在以A、B、C、M、、、、、这八个点中的四个点为顶点的平行四边形中，求其中一个不是菱形的平行四边形的面积。
【答案】（1）（-4,0）（-1,0）（0，1）；（2）
；（3）18．
【解析】
试题（1）先分别令y=0，x=0解方程再写出就可；
（2）先求出点A、B、C的坐标关于坐标原点O的对称点再利用待定系数法求出解析式；
（3）如图，取四点A、M、
、
，连接AM、M、、A、M，先判断连接的四边形为平行四边形但不是菱形，再求面积即可．
试题解析：（1）令y=0得x
+5x+4=0 解得
令x=0得y=4
∴点A、B、C的坐标分别为（-4,0）（-1,0）（0，4）
（2）点A、B、C的坐标关于坐标原点O的对称点分别为（4,0）（1,0）（0，-4）
∴设所求抛物线的函数表达式为
将（4,0）（1,0）带入上式得
∴所求抛物线的函数表达式为
（3）如图，取四点A、M、、，连接AM、M、、A、M，
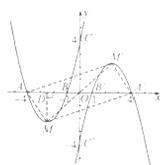
有中心对称性可知，M过点O，OA=O,OM=O ∴四边形AM
是平行四边形．
又知A与M不垂直 ∴四边形AM不是菱形．
过点M作MD⊥x轴于点D。
∵
=
． ∴点M（
）
有∵A(-4，0) (4，0) ∴A=8，MD=
∴
=
18．
练习册系列答案
相关题目
