Question

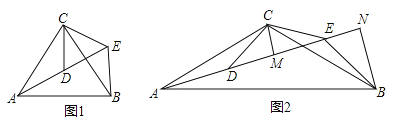
【题目】（2016山东省菏泽市）如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．

（1）如图1，若∠CAB=∠CBA=∠CDE=∠CED=50°

①求证：AD=BE；

②求∠AEB的度数．

（2）如图2，若∠ACB=∠DCE=120°，CM为△DCE中DE边上的高，BN为△ABE中AE边上的高，试证明：AE=CM+BN．

Answer 1

【答案】（1）①证明见解析；②80°；（2）证明见解析．

【解析】试题（1）①通过角的计算找出∠ACD=∠BCE，再结合△ACB和△DCE均为等腰三角形可得出“AC=BC，DC=EC”，利用全等三角形的判定（SAS）即可证出△ACD≌△BCE，由此即可得出结论AD=BE；

②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC，再通过角的计算即可算出∠AEB的度数；

（2）根据等腰三角形的性质结合顶角的度数，即可得出底角的度数，利用（1）的结论，通过解直角三角形即可求出线段AD、DE的长度，二者相加即可证出结论．

试题解析：（1）①证明：∵∠CAB=∠CBA=∠CDE=∠CED=50°，∴∠ACB=∠DCE=180°﹣2×50°=80°．

∵∠ACB=∠ACD+∠DCB，∠DCE=∠DCB+∠BCE，∴∠ACD=∠BCE．

∵△ACB和△DCE均为等腰三角形，∴AC=BC，DC=EC．

在△ACD和△BCE中，∵AC=BC，∠ACD=∠BCE，DC=EC，∴△ACD≌△BCE（SAS），∴AD=BE．

②解：∵△ACD≌△BCE，∴∠ADC=∠BEC．

∵点A，D，E在同一直线上，且∠CDE=50°，∴∠ADC=180°﹣∠CDE=130°，∴∠BEC=130°．

∵∠BEC=∠CED+∠AEB，且∠CED=50°，∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°．

（2）证明：∵△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=120°，∴∠CDM=∠CEM=×（180°﹣120°）=30°．

∵CM⊥DE，∴∠CMD=90°，DM=EM．

在Rt△CMD中，∠CMD=90°，∠CDM=30°，∴DE=2DM=2×=CM．

∵∠BEC=∠ADC=180°﹣30°=150°，∠BEC=∠CEM+∠AEB，∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°，∴∠BEN=180°﹣120°=60°．

在Rt△BNE中，∠BNE=90°，∠BEN=60°，∴BE==BN．

∵AD=BE，AE=AD+DE，∴AE=BE+DE=CM+BN．