题目内容
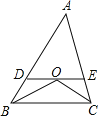
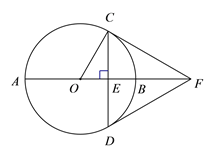
【题目】如图,![]() 是⊙
是⊙![]() 的直径,弦
的直径,弦![]()
![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接DF.
,连接DF.
(1)求证:DF是⊙![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() =30°,
=30°,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】(1) 连接OD,由垂径定理证OF为CD的垂直平分线,得CF=DF,∠CDF=∠DCF,由∠CDO=∠OCD,再证∠CDO +∠CDB=∠OCD+∠DCF=90°,可得OD⊥DF,结论成立.
(2) 由∠OCF=90°, ∠BCF=30°,得∠OCB=60°,再证ΔOCB为等边三角形,得∠COB=60°,可得∠CFO=30°,所以FO=2OC=2OB,FB=OB= OC =2,在直角三角形OCE中,解直角三角形可得CE,再推出CD=2CE.
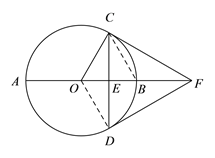
(1)证明:连接OD
∵CF是⊙O的切线
∴∠OCF=90°
∴∠OCD+∠DCF=90°
∵直径AB⊥弦CD
∴CE=ED,即OF为CD的垂直平分线
∴CF=DF
∴∠CDF=∠DCF
∵OC=OD,
∴∠CDO=∠OCD
∴∠CDO +∠CDB=∠OCD+∠DCF=90°
∴OD⊥DF
∴DF是⊙O的切线
(2)解:连接OD
∵∠OCF=90°, ∠BCF=30°
∴∠OCB=60°
∵OC=OB
∴ΔOCB为等边三角形,
∴∠COB=60°
∴∠CFO=30°
∴FO=2OC=2OB
∴FB=OB= OC =2
在直角三角形OCE中,∠CEO=90°∠COE=60°
![]()
∴CF![]()
∴CD=2 CF![]()

【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从八、九两个年级各随机抽取![]() 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:
八年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
九年级 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按如下分数段整理、描述这两组样本数据:
|
|
|
|
|
| |
八年级 | 0 | 0 | 1 | 11 | 1 | |
九年级 | 1 | 0 | 0 | 7 |
(说明:成绩![]() 分及以上为体质健康优秀,
分及以上为体质健康优秀,![]() ~
~![]() 分为体质健康良好,
分为体质健康良好,![]() ~
~![]() 分为体质健康合格,
分为体质健康合格,![]() 分以下为体质健康不合格)
分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 |
|
|
| 33.6 |
九年级 |
|
| 52.1 |
请将以上两个表格补充完整;
得出结论
(1)估计九年级体质健康优秀的学生人数为__________;
(2)可以推断出_______年级学生的体质健康情况更好一些,理由为_________________.(至少从两个不同的角度说明推断的合理性).