题目内容
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣8,点C在数轴上表示的数是10,若线段 AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的数度也向右匀速运动.
![]()
(1)运动t秒后,点B表示的数是 ;点C表示的数是 ;(用含有t的代数式表示)
(2)求运动多少秒后,BC=4(单位长度);
(3)P是线段AB上一点,当B点运动到线段CD上,且点P不在线段CD上时,是否存在关系式 BD﹣AP=3PC.若存在,求线段PD的长;若不存在,请说明理由.
【答案】(1)-6+6t,10+2t;(2)运动3秒或5秒后BC=4;(3)存在关系式BD﹣AP=3PC,此时PD=5.
【解析】
(1)根据数轴上的两点之间距离公式即可求出答案;
(2)设运动ts后,根据BC=4,分点B在点C的左、右两侧两种情况,列出方程即可求出t的值;
(3)假设存在点P,使BD﹣AP=3PC.设BD=x,则CB=4-x,AC=2-(4-x)=x-2,根据题意可知点P只能在C点左侧,得出AP+CP=AC,再结合BD﹣AP=3PC可求得PC的长,从而可求出此时PD的长.
解:(1)AB=2,CD=4,点A在数轴上表示的数是﹣8,点C在数轴上表示的数是10,
∴未运动之前,点B表示的数为-6,点D表示的数为14,
∴向右运动t秒后,点B,点C表示的数分别为-6+6t,10+2t.
故答案为:-6+6t,10+2t;
(2)设运动t秒后,BC=4,由题意可知:
当点B在点C左侧时,
∴(10+2t)-(-6+6t)=4,解得t=3;
当点B在点C的右侧时,
或(-6+6t)-(10+2t)=4,解得t=5,
答:运动3秒或5秒后BC=4;
(3)存在关系式BD-AP=3PC.理由如下:
设BD=x,则CB=4-x,AC=2-(4-x)=x-2,
∵点B运动到线段CD上,点P不在线段CD上,如图,点P只能在点C的左侧,
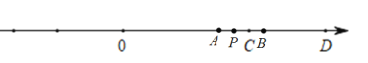
∴AP+CP=AC,
∵BD-AP=3PC,
∴BD=x=AP+PC+2PC=AC+2PC=x-2+2PC,
∴PC=1,
∴当PC=1时,BD-AP=3PC,
即PD=PC+CD=1+4=5.