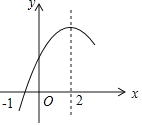题目内容
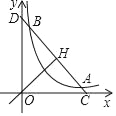
【题目】如图,已知抛物线![]()
![]() 与
与![]() 轴交于A(-1,0),B(3,0)两点,与
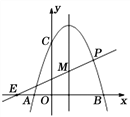
轴交于A(-1,0),B(3,0)两点,与![]() 轴交于点C(0,3),动点P在抛物线上,直线PE与抛物线的对称轴交于点M,点E的坐标为(-2,0).
轴交于点C(0,3),动点P在抛物线上,直线PE与抛物线的对称轴交于点M,点E的坐标为(-2,0).
(1)求抛物线的函数表达式;
(2)若P与C关于抛物线的对称轴对称,求直线PE的函数表达式;
(3)若PM=![]() EM,求点P的坐标.
EM,求点P的坐标.
【答案】(1) y=-x2+2x+3;(2)y=![]() ;(3)点P的坐标为(
;(3)点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】分析:(1)把点A、B、C的坐标代入抛物线![]() 中,解出即可.
中,解出即可.
(2)设PE的函数表达式y=kx+m,根据题意算出P点坐标,把P、E的坐标代入y=kx+m中,求出k、m的值即可.
(3)根据相似三角形的性质即可解答.
详解:(1) ∵抛物线![]() 与x轴交于A(-1,0),B(3,0),
与x轴交于A(-1,0),B(3,0),
∴可设抛物线的函数表达式为![]() ,
,
将C(0,3)代入,得:3=a×(0+1)(0-3),∴a=-1,
∴抛物线的函数表达式为y=-(x+1)(x-3).
即y=-x2+2x+3 .

(2) ∵抛物线的对称轴为x=![]() ,
,
∴点C(0,3)关于对称轴x=1对称的点为(2,3),
∴由题意知,此时点P的坐标为(2,3),
设直线PE的函数表达式为y=kx+m,
将P(2,3),E(-2,0)代入,
得: ![]() 解得:
解得: .
.
∴直线PE的函数表达式为y=![]() .
.
(3)如图,设对称轴x=1与x轴的交点为F,过P作PH垂直对称轴x=1于点H,
∵对称轴x=1与x轴垂直,
∴Rt△PMH∽Rt△EMF,∴![]() ,
,
设动点P的坐标为(x,y),
∵动点P可能在对称轴x=1的左侧或右侧的抛物线上,∴PH=|x-1|![]() ,
,
又EF=3,PM=![]() EM,
EM,
∴![]() ,∴x-1=
,∴x-1=![]() ,x=
,x=![]() 或x=
或x=![]() ,
,
当x=![]() 时,y=-(
时,y=-(![]() +1)(
+1)( ![]() -3)=
-3)=![]() ,
,
当x=![]() 时,y=-(
时,y=-(![]() +1)(
+1)( ![]() -3)=
-3)= ![]() ,
,
∴所求点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

【题目】 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)①表中a的值为 ,中位数在第 组;
②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |