题目内容
【题目】某服装店准备购进甲、乙两种服装出售,甲种每件售价120元,乙种每件售价90元.每件甲服装的进价比乙服装的进价贵20元,购进3件甲服装的费用和购进4件乙服装的费用相等,现计划购进两种服装共100件,其中甲种服装不少于65件.
(1)甲种服装进价为 元/件,乙种服装进价为 元/件;
(2)若购进这100件服装的费用不得超过7500元.
①求甲种服装最多购进多少件?
②该服装店对甲种服装每件降价![]() 元,乙种服装价格不变,如果这100件服装都可售完,那么该服装店如何进货才能获得最大利润?
元,乙种服装价格不变,如果这100件服装都可售完,那么该服装店如何进货才能获得最大利润?
【答案】(1)80;60;(2)①甲种服装最多购进75件;②当![]() 时,购进甲种服装75件,乙种服装25件;当
时,购进甲种服装75件,乙种服装25件;当![]() 时,所有进货方案获利相同;当
时,所有进货方案获利相同;当![]() 时,购进甲种服装65件,乙种服装35件.
时,购进甲种服装65件,乙种服装35件.
【解析】
(1)设乙服装的进价y元/件,则甲种服装进价为(y+20)元/件,根据题意列方程即可解答;
(2)①设甲种服装购进x件,则乙种服装购进(100-x)件,然后根据购进这100件服装的费用不得超过7500元,列出不等式组解答即可;
②首先求出总利润W的表达式,然后针对a的不同取值范围进行讨论,分别确定其进货方案.
(1)设乙服装的进价y元/件,则甲种服装进价为![]() 元/件,根据题意得:
元/件,根据题意得:
![]() ,
,
解得![]() ,
,
即甲种服装进价为80元/件,乙种服装进价为60元/件;
故答案为:80;60;
(2)①设计划购买![]() 件甲种服装,则购买
件甲种服装,则购买![]() 件乙种服装,根据题意得
件乙种服装,根据题意得
![]() ,解得
,解得![]() ,
,
![]() 甲种服装最多购进75件;
甲种服装最多购进75件;
②设总利润为![]() 元,购进甲种服装
元,购进甲种服装![]() 件.
件.
则![]() ,且
,且![]() ,
,
当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而增大,故当
的增大而增大,故当![]() 时,
时,![]() 有最大值,即购进甲种服装75件,乙种服装25件;
有最大值,即购进甲种服装75件,乙种服装25件;
当![]() 时,所有进货方案获利相同;
时,所有进货方案获利相同;
当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而减少,故当
的增大而减少,故当![]() 时,
时,![]() 有最大值,即购进甲种服装65件,乙种服装35件.
有最大值,即购进甲种服装65件,乙种服装35件.

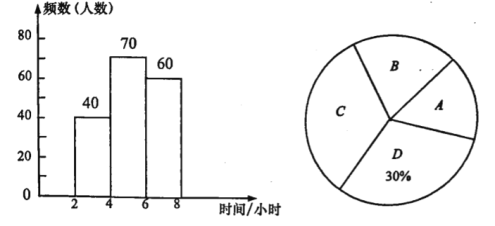
【题目】某区对即将参加中考的初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查的样本为 ,样本容量为 ;
(2)在频数分布表中,组距为 ,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,计算抽样中视力正常的百分比.