题目内容
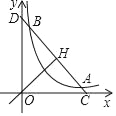
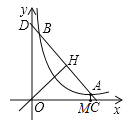
【题目】如图,已知直线y=﹣x+b(b>0)与其垂线y=x交于H,与双曲线c:y=![]() (k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(k>0)在第一象限交于A,B,与两坐标轴交于C,D.
(1)当A的坐标为(2,1)时,求k的值和OH的长;
(2)若CH2﹣HA2=4,求双曲线c的方程.
【答案】(1)OH=![]() ;(2)设双曲线c的方程为y=
;(2)设双曲线c的方程为y=![]() .
.
【解析】分析:(1)将A(2,1)代入y=![]() ,可得k=2,过A作AM⊥x轴于M,则AM=MC=1,OM=2,可得OC=OM+MC=3,依据∠HOC=45°,即可得到OH=
,可得k=2,过A作AM⊥x轴于M,则AM=MC=1,OM=2,可得OC=OM+MC=3,依据∠HOC=45°,即可得到OH=![]() OC=
OC=![]() ;
;
(2)设点A的坐标为(x,y)且x>y,则OC=OM+MC=x+y,OH=HC=![]() OC=
OC=![]() (x+y),进而得出HA=HC﹣AC=
(x+y),进而得出HA=HC﹣AC=![]() (x﹣y),根据CH2﹣HA2=[
(x﹣y),根据CH2﹣HA2=[![]() (x+y)]2﹣[
(x+y)]2﹣[![]() (x﹣y)]2=2xy=2k=4,即可得到k的值.
(x﹣y)]2=2xy=2k=4,即可得到k的值.
详解:(1)将A(2,1)代入y=![]() ,可得:k=2×1=2,
,可得:k=2×1=2,
过A作AM⊥x轴于M,则AM=MC=1,OM=2,∴OC=OM+MC=3.
∵∠HOC=45°,∴OH=![]() OC=
OC=![]() ;
;
(2)设点A的坐标为(x,y)且x>y,则OC=OM+MC=x+y,OH=HC=![]() OC=
OC=![]() (x+y).
(x+y).
又∵AC=![]() AM=
AM=![]() y,∴HA=HC﹣AC=
y,∴HA=HC﹣AC=![]() (x﹣y).
(x﹣y).
∵CH2﹣HA2=[![]() (x+y)]2﹣[
(x+y)]2﹣[![]() (x﹣y)]2=2xy=2k=4,∴k=2,
(x﹣y)]2=2xy=2k=4,∴k=2,
∴双曲线c的方程为y=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目