题目内容
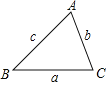
【题目】如图，在四边形ABCD中，∠ABC=90°，∠BAD=60°，AC=AD，AC平分∠BAD，M，N分别为AC，CD的中点，BM的延长线交AD于点E，连接MN，BN．对于下列四个结论：①MN∥AD；② BM=MN；③△BAE≌△ACB；④AD=
BN，其中正确结论的序号是( )
A. ①②③④ B. ①②③ C. ①②④ D. ①②
【答案】C
【解析】分析： 根据三角形中位线定理，直角三角形斜边上的中线一一判断即可.
详解：①在△CAD中，∵M、N分别是AC、CD的中点，∴MN∥AD，正确.
②在△CAD中，∵M、N分别是AC、CD的中点，∴MN∥AD，MN=
AD，
在RT△ABC中，∵M是AC中点，∴BM=AC，∵AC=AD，∴BM=MN.正确.
③错误.
④设AM=x,∵∠BAD=60°，AC平分∠BAD，∴∠BAC=∠DAC=30°，∵∠ABC=90°，M为AC的中点，∴BM=AM=x，∴∠CMB=2∠BAC=60°，∵AC=AD，∴AD=2x，∵M，N分别为AC，CD的中点，∴MN=AD=x,∠CMN=∠DAC=30°，∴∠BMN=90°，∴BN=
，∴
BN=AD.故正确.
故答案为：C.
练习册系列答案
相关题目
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，把超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值（单位：克） | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
（1）若每袋食品的标准质量为450克，则抽样检测的20袋食品的总质量是多少克？
（2）若该种食品的合格标准为450±5克，求该种食品抽样检测的合格率？
