Question

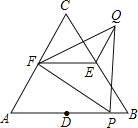
【题目】已知：如图，AD是△ABC的高，AD的垂直平分线分别交AB，AC于点E，F．

（1）求证：∠B＝∠AED；

（2）若添加条件：DE＝DF．求证：∠B＝∠C．

Answer 1

【答案】（1）见详解；（2）见详解

【解析】

（1）证明△AHE≌△DHE（SAS），得出∠AEH＝∠DEH．AE＝DE，证出EF∥BC，得出∠AEH＝∠B，即可得出结论；

（2）证明DE，DF分别是Rt△ADB，Rt△ADC的斜边AB，AC上的中线，得出DE＝AB，DF＝AC．证出AB＝AC，即可得出∠B＝∠C．

（1）证明：∵EF是AD的中垂线，

∴AH＝DH，∠AHE＝∠DHE＝90°，

在△AEH和△DEH中，

∴△AHE≌△DHE（SAS），

∴∠AEH＝∠DEH．AE＝DE，

∵AD是△ABC的高，

∴EF∥BC，

∴∠AEH＝∠B，

∴∠B＝∠AED．

（2）证明：由（1）得：EF∥BC，AH＝DH，

∴AE＝BE，AF＝CF，

∴DE，DF分别是Rt△ADB，Rt△ADC的斜边AB，AC上的中线，

∴DE＝AB，DF＝AC．

∵DE＝DF，

∴AB＝AC，

∴∠B＝∠C．