题目内容
【题目】如图,![]() 、
、![]() 分别是边长
分别是边长![]() 为的等边
为的等边![]() 的边
的边![]() ,
,![]() 上的动点,点
上的动点,点![]() 从顶点
从顶点![]() ,点
,点![]() 从顶点
从顶点![]() 同时出发,分别沿
同时出发,分别沿![]() ,
,![]() 边运动,点
边运动,点![]() 到点
到点![]() 停止,点
停止,点![]() 到点
到点![]() 停止.社运动时间为
停止.社运动时间为![]() 秒,他们的速度都为
秒,他们的速度都为![]() .
.

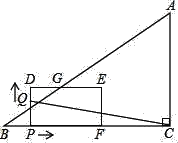
(1)连接![]() ,
,![]() 相交于
相交于![]() ,在点
,在点![]() ,
,![]() 的运动过程中
的运动过程中![]() 的大小是否变化?若变化,说明理由;若不变,求出它的度数;
的大小是否变化?若变化,说明理由;若不变,求出它的度数;
(2)当![]() 取何值时,
取何值时,![]() 是直角三角形.
是直角三角形.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)利用等边三角形的性质可证明△APC≌△BQA,则可求得∠BAQ=∠ACP,再利用三角形外角的性质可证得∠CMQ=60°;
(2)可用t分别表示出BP和BQ,分∠BPQ=90°和∠BPQ=90°两种情况,分别利用直角三角形的性质可得到关于t的方程,则可求得t的值;
(1)∵△ABC为等边三角形,

∴AB=AC,∠B=∠PAC=60°,
∵点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
∴AP=BQ,
在△APC和△BQA中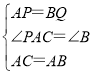 ,
,
∴△APC≌△BQA(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠CAQ+∠ACP=∠BAQ+∠CAQ=∠BAC=60°,
∴在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°;
(2)∵运动时间为ts,则AP=BQ=t,
∴PB=4-t,
①当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,
∴4-t=2t,解得![]() ,
,
②当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2PB,
∴t=2(4-t),解得![]() ,
,
∴当t为![]() s或
s或![]() s时,△PBQ为直角三角形;
s时,△PBQ为直角三角形;

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
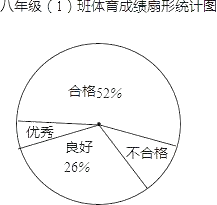
应用题点拨系列答案【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .