题目内容
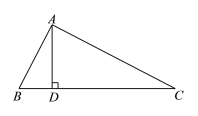
【题目】如图,钝角△ABC中,AB=AC,BC=2![]() ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
(1)求证:EF⊥AC.
(2)连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.

【答案】(1)见解析;(2)![]()
【解析】
(1)因为EF为圆0的切线,故由此想到连接OE,得到∠OEF=90°,再根据OB和OE的关系找出∠OEB=∠C,判断出OE平行于AC,即可以得出EF⊥AC.
(2)连接DE、DF,设圆的半径为r,利用直径所对的圆周角是直角,得出∠DEB为直角,再根据 EF⊥AC,OE⊥AB,角与角之间的关系可以求出∠EDF为直角,利用勾股定理求出BE、EC的长,再根据BE+EC=![]() 可以求出圆O的半径.
可以求出圆O的半径.
(1)证明:连接OE,如图,
∵OB=OE,
∴∠B=∠OEB,
∵AB=AC,
∴∠B=∠C,
∴∠OEB=∠C,
∴OE∥AC,
∵EF为切线,
∴OE⊥EF,
∴EF⊥AC;
(2)解:连接DE,如图,设⊙O的半径长为r,
∵BD为直径,
∴∠BED=90°,
在Rt△BDE中,∵∠B=30°,
∴DE=![]() BD=r,BE=
BD=r,BE=![]() r,
r,
∵DF∥BC,
∴∠EDF=∠BED=90°,
∵∠C=∠B=30°,
∴∠CEF=60°,
∴∠DFE=∠CEF=60°,
在Rt△DEF中,DF=![]() r,
r,
∴EF=2DF=![]() r,
r,
在Rt△CEF中,CE=2EF=![]() r,
r,
而BC=2![]() ,
,
∴![]() r+
r+![]() r=2
r=2![]() ,解得r=
,解得r=![]() ,
,
即⊙O的半径长为![]() .
.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目