题目内容
【题目】已知一次函数![]() 的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
A.0B.1C.2D.大于2的整数
【答案】A
【解析】
解:把点(98,19)代入y=ax+b,得98a+b=19;把(p,0),(0,q)也代入y=ax+b,得b=q,a=-![]() .所以19p=-98q+pq,则q=
.所以19p=-98q+pq,则q=![]() ,p是质数,q是正整数,再利用整除的性质讨论即可.
,p是质数,q是正整数,再利用整除的性质讨论即可.
解:把点(98,19)代入y=ax+b,得98a+b=19;
把(p,0),(0,q)也代入y=ax+b,得b=q,a=-![]() .
.
所以19p=-98q+pq,
则q=![]() ,p是质数,q是正整数,分子只有三个因数即1、19、p,则p-98只能等于1、19或p,解的p都不是质数.
,p是质数,q是正整数,分子只有三个因数即1、19、p,则p-98只能等于1、19或p,解的p都不是质数.
所以满足条件的所有一次函数的个数为0.
故答案为A.
本题考查了一次函数的性质,点在图象上,则点的横纵坐标满足解析式.也考查了质数的概念和整数的整除性质.

 期末冲刺100分创新金卷完全试卷系列答案
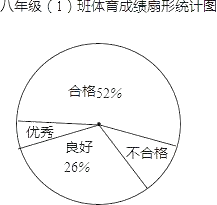
期末冲刺100分创新金卷完全试卷系列答案【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .
【题目】某校团委组织“阳光助残”献爱心捐款活动,九年级(2)班学生捐款如表:
捐款金额(元) | 5 | 10 | 15 | 20 |
人数(人) | 13 | 16 | 17 | 10 |
学生捐款的中位数和众数是( )
A. 10元,15元 B. 15元,15元 C. 10元,20元 D. 16元,17元