��Ŀ����
����Ŀ����һ��������ı���ȫͿ����ɫ��
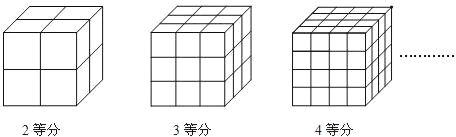
��1����������������2�ȷ֣�Ȼ���صȷ��߰��������п����ܹ��õ�8��С�����壬������3�汻Ϳ����ɫ����a������a=�� ����
��2�������������������ȷ֣�Ȼ���صȷ��߰��������п����ܹ��õ�27��С�����壮����ЩС����������3����Ϳ����ɫ����a���������涼û��Ϳɫ����b������a+b=�� ����
��3����������������4�ȷ֣�Ȼ���صȷ��߰��������п����ܹ��õ�64��С�����壮����ЩС����������2����Ϳ����ɫ����c���������涼û��Ϳɫ����b������c+b=�� ����
��4����������������n�ȷ֣�Ȼ���صȷ��߰��������п����ܹ��õ��� ����С�����壮����ЩС����������2����Ϳ����ɫ����c���������涼û��Ϳɫ����b������c+b=�� ����
���𰸡���1��8����2��9����3��32����4��![]() ��
��![]() ��
��
��������
��������������ʿɷ��ֶ��㴦��С��������Ϳɫ����������λ�����ϵ�С��������Ϳɫ��Ϳɫλ�ڱ������ĵ�һ��Ϳɫ�����������ĵ�ûͿɫ�����˿ɵõ���1������ȷ�ʱ������С���������Ϳɫ�������2�������ȷ�ʱ������С���������Ϳɫ�������3�����ĵȷ�ʱ������С���������Ϳɫ�������4��������֪ͼ����û��Ϳɫ��С�����θ����ó��仯���ɽ����ó��𰸣�
�⣺��1�����汻Ϳɫ����8������a=8��
��2�����汻Ϳɫ����8�������涼û��Ϳɫ��1����a+b=8+1=9��
��3�����汻Ϳ�ɺ�ɫ��24�������涼û��Ϳɫ��8����b+c=24+8=32��
��4�������Ͽɷ��ֹ��ɣ��ܹ��õ�n3��С�����壬����Ϳɫc=12��n��2�������������Ϳɫ��n��2��3����b+c=12��n��2��+��n��2��3��
�ʴ�Ϊ��8��9��32��n3��12��n��2��+��n��2��3��

 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�