题目内容
【题目】综合题
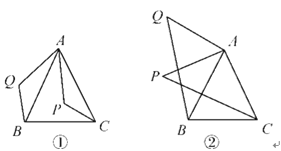
(1)【阅读发现】如图①,在△ABC中,∠ACB=45°,AD⊥BC于点D,E为AD上一点,且DE=BD,可知AB=CE.
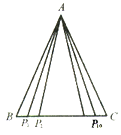
(2)【类比探究】如图②,在正方形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F.判断AF与BE的数量关系,并加以证明.
(3)【推广应用】在图②中,若AB=4,BF= ![]() ,则△AGE的面积为 .
,则△AGE的面积为 . 
【答案】
(1)
解:∵AD⊥BC,∠ACB=45°,
∴∠ADB=∠CDE=90°,△ACD是等腰直角三角形,
∴AD=CD,
在△ABD和△CED中, 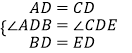 ,
,
∴△ABD≌△CED(SAS),
∴AB=CE;
(2)
解:AF=BE;理由如下:
∵正方形ABCD中,AB=BC=AD,∠BAD=90°,∠ABF=∠BCE=45°,AC⊥BD,OA=OB=OC,
∵AG⊥BE,
∴∠FAD+∠AFO=90°,
∵AG⊥BE,
∴∠FAO+∠AEG=90°,
∴∠AFO=∠AEG,
∵∠AFB=∠FAO+90°,
∴∠AFB=∠BEC,
在△ABF和△BCE中, 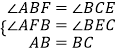 ,
,
∴△ABF≌△BCE(AAS),
∴AF=BE;
(3)![]()
【解析】【推广应用】解:∵AB=AD=4,∠BAD=90°,
∴BD= ![]() =4
=4 ![]() ,
,
∴OA=OB=OC= ![]() BD=2
BD=2 ![]() ,
,
∵BF= ![]() ,
,
∴OF=OB﹣BF= ![]() ,
,
∴AF= ![]() =
= ![]() ,
,
由角的互余性质得:∠OAF=∠OBE,
在△OBE和△OAF中, 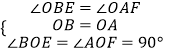 ,
,
∴△OBE≌△OAF(ASA),
∴OE=OE= ![]() ,
,
∴AE=OA+OE=3 ![]() ,
,
∵∠OAF=∠GAE,∠AOF=∠AGE=90°,
∴△AOF∽△AGE,
∴ ![]() ,即
,即 ![]() ,
,
解得:GE= ![]() ,AG=
,AG= ![]() ,
,
∴△AGE的面积= ![]() AGGE=
AGGE= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】掌握等腰直角三角形和勾股定理的概念是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.