题目内容
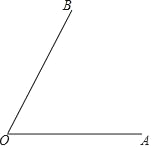
【题目】如图,∠AOB=60°,分别引射线OC、OD、OE,使OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=20°,请依题意补全图形,并求∠BOE的度数;
(2)若∠BOC=α(其中α是小于60°的锐角),请直接写出∠BOE的度数(用含α的代数式表示).
【答案】(1)第一种情况:当CO在∠AOB外部时,∠BOE=25°;第二种情况:当CO在∠AOB内部时,∠BOE==35°;(2)①当CO在∠AOB外部时,第一种情况:当CO在∠AOB外部时,∠BOE=30°﹣![]() α;第二种情况:当CO在∠AOB内部时,∠BOE30°+
α;第二种情况:当CO在∠AOB内部时,∠BOE30°+![]() α.
α.
【解析】
(1)分为两种情况:当CO在∠AOB外部时和当CO在∠AOB内部时,求出∠AOC、∠BOD的度数,求出∠AOD,根据角平分线求出∠AOE,即可求出答案;
(2)分为两种情况:当CO在∠AOB外部时和当CO在∠AOB内部时,求出∠AOC、∠BOD的度数,求出∠AOD,根据角平分线求出∠AOE,即可求出答案.
(1)第一种情况:当CO在∠AOB外部时,

∵∠AOB=60°,∠BOC=20°,
∴∠AOC=∠AOB+∠BOC=60°+20°=80°,
∵OD平分∠BOC,
∴∠COD=∠BOD=![]() ∠BOC=10°,
∠BOC=10°,
∴∠AOD=∠AOB+∠BOD=60°+10°=70°,
∵OE平分∠AOD,
∴∠AOE=![]() ∠AOD=35°,
∠AOD=35°,
∴∠BOE=∠AOB﹣∠AOE=60°﹣35°=25°;
第二种情况:当CO在∠AOB内部时,
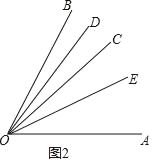
∵∠AOB=60°,∠BOC=20°,
∴∠AOC=∠AOB﹣∠BOC=60°﹣20°=40°,
∵OD平分∠BOC,
∴∠COD=∠BOD=![]() ∠BOC=10°,
∠BOC=10°,
∴∠AOD=∠AOB﹣∠BOD=60°﹣10°=50°,
∵OE平分∠AOD,
∴∠AOE=![]() ∠AOD=25°,
∠AOD=25°,
∴∠BOE=∠AOB﹣∠AOE=60°﹣25°=35°;
(2)①当CO在∠AOB外部时,第一种情况:当CO在∠AOB外部时,
∵∠AOB=60°,∠BOC=α,
∴∠AOC=∠AOB+∠BOC=60°+α,
∵OD平分∠BOC,
∴∠COD=∠BOD=![]() ∠BOC=
∠BOC=![]() ,
,
∴∠AOD=∠AOB+∠BOD=60°+![]() ,
,
∵OE平分∠AOD,
∴∠AOE=![]() ∠AOD=30°+
∠AOD=30°+![]() α,
α,
∴∠BOE=∠AOB﹣∠AOE=60°﹣(30°+![]() α)=30°﹣
α)=30°﹣![]() α;
α;
第二种情况:当CO在∠AOB内部时,
∵∠AOB=60°,∠BOC=α,
∴∠AOC=∠AOB﹣∠BOC=60°﹣α,
∵OD平分∠BOC,
∴∠COD=∠BOD=![]() ∠BOC=
∠BOC=![]() ,
,
∴∠AOD=∠AOB﹣∠BOD=60°﹣![]() ,
,
∵OE平分∠AOD,
∴∠AOE=![]() ∠AOD=30°﹣
∠AOD=30°﹣![]() α,
α,
∴∠BOE=∠AOB﹣∠AOE=60°﹣(30°﹣![]() α)=30°+
α)=30°+![]() α.
α.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案