题目内容
【题目】【特例发现】如图1,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.求证:EP=FQ.
【延伸拓展】如图2,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作Rt△ABE和Rt△ACF,射线GA交EF于点H.若AB=kAE,AC=kAF,请思考HE与HF之间的数量关系,并直接写出你的结论.
【深入探究】如图3,在△ABC中,G是BC边上任意一点,以A为顶点,向△ABC外作任意△ABE和△ACF,射线GA交EF于点H.若∠EAB=∠AGB,∠FAC=∠AGC,AB=kAE,AC=kAF,上一问的结论还成立吗?并证明你的结论.
【应用推广】在上一问的条件下,设大小恒定的角∠IHJ分别与△AEF的两边AE、AF分别交于点M、N,若△ABC为腰长等于4的等腰三角形,其中∠BAC=120°,且∠IHJ=∠AGB=θ=60°,k=2;
求证:当∠IHJ在旋转过程中,△EMH、△HMN和△FNH均相似,并直接写出线段MN的最小值(请在答题卡的备用图中补全作图).

【答案】(1)证明参见解析;(2)HE=HF;(3)成立,证明参见解析;(4)证明参见解析,MN最小值为1.
【解析】
试题分析:(1)特例发现:易证△AEP≌△BAG,△AFQ≌△CAG,即可求得EP=AG,FQ=AG,即可解题;(2)延伸拓展:过点E、F作射线GA的垂线,垂足分别为P、Q.易证△ABG∽△EAP,△ACG∽△FAQ,得到PE=![]() AG,FQ=
AG,FQ=![]() AG,∴PE=FQ,然后证明△EPH≌△FQH,即可得出HE=HF;(3)深入探究:判断△PEA∽△GAB,得到PE=
AG,∴PE=FQ,然后证明△EPH≌△FQH,即可得出HE=HF;(3)深入探究:判断△PEA∽△GAB,得到PE=![]() AG,△AQF∽△CGA,FQ=,得到FQ=
AG,△AQF∽△CGA,FQ=,得到FQ=![]() AG,再判断△EPH≌△FQH,即可得出HE=HF;(4)应用推广:由前一个结论得到△AEF为正三角形,再依次判断△MHN∽△HFN∽△MEH,即可得出结论.
AG,再判断△EPH≌△FQH,即可得出HE=HF;(4)应用推广:由前一个结论得到△AEF为正三角形,再依次判断△MHN∽△HFN∽△MEH,即可得出结论.
试题解析:(1)特例发现,如图:
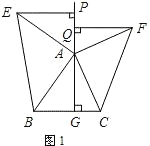 ∵∠PEA+∠PAE=90°,∠GAB+∠PAE=90°,∴∠PEA=∠GAB,∵∠EPA=∠AGB,AE=AB,∴△PEA≌△GAB,∴PE=AG,同理,△QFA≌△GAC,∴FQ=AG,∴PE=FQ;
∵∠PEA+∠PAE=90°,∠GAB+∠PAE=90°,∴∠PEA=∠GAB,∵∠EPA=∠AGB,AE=AB,∴△PEA≌△GAB,∴PE=AG,同理,△QFA≌△GAC,∴FQ=AG,∴PE=FQ;
(2)延伸拓展,如图:

∵∠PEA+∠PAE=90°,∠GAB+∠PAE=90°,∴∠PEA=∠GAB,∴∠EPA=∠AGB,∴△PEA∽△GAB,∴![]() ,∵AB=kAE,∴
,∵AB=kAE,∴![]() ,∴PE=
,∴PE=![]() AG,同理,△QFA∽△GAC,∴
AG,同理,△QFA∽△GAC,∴![]() ,∵AC=kAF,∴FQ=
,∵AC=kAF,∴FQ=![]() AG,∴PE=FQ,∵EP∥FQ,∴∠EPH=∠FQH,∵∠PHE=∠QHF,∴△EPH≌△FQH,∴HE=HF;
AG,∴PE=FQ,∵EP∥FQ,∴∠EPH=∠FQH,∵∠PHE=∠QHF,∴△EPH≌△FQH,∴HE=HF;
(3)深入探究,如图2,

在直线AG上取一点P,使得∠EPA═∠AGB,作FQ∥PE,∵∠EAP+∠BAG=180°﹣∠AGB,∠ABG+∠BAG=180°﹣∠AGB,∴∠EAP=∠ABG,∵∠EPA=∠AGB,∴△APE∽△BGA,∴![]() ,∵AB=kAE,∴PE=
,∵AB=kAE,∴PE=![]() AG,由于∠FQA=∠FAC=∠AGC=180°﹣∠AGB,同理可得,△AQF∽△CGA,∴
AG,由于∠FQA=∠FAC=∠AGC=180°﹣∠AGB,同理可得,△AQF∽△CGA,∴![]() ,∵AC=kAF,∴FQ=
,∵AC=kAF,∴FQ=![]() AG,∴EP=FQ,∵EP∥FQ,∴∠EPH=∠FQH,∵∠PHE=∠QHF,∴△EPH≌△FQH,∴HE=HF;
AG,∴EP=FQ,∵EP∥FQ,∴∠EPH=∠FQH,∵∠PHE=∠QHF,∴△EPH≌△FQH,∴HE=HF;
(4)应用推广,如图3,
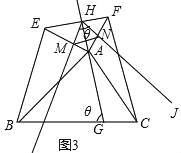
在前面条件及结论,得到,点H是EF中点,∴AE=AF,∵∠EAB=∠AGB,∠FAC=∠AGC∴∠EAB+∠FAC=180°∴∠EAF=360°﹣(∠EAB+∠FAC)﹣∠BAC=60°,∴△AEF为正三角形.又H为EF中点,∴∠EHM+∠IHJ=120°,∠IHJ+∠FHN=120°,∴∠EHM=∠FHN.∵∠AEF=∠AFE,∴△HEM∽△HFN,∴![]() ,∵EH=FH,∴
,∵EH=FH,∴![]() ,且∠MHN=∠HFN=60°,∴△MHN∽△HFN,∴△MHN∽△HFN∽△MEH,在△HMN中,∠MHN=60°,根据三角形中大边对大角,∴要MN最小,只有△HMN是等边三角形,∴∠AMN=60°,∵∠AEF=60°,MN∴MN∥EF,∵△AEF为等边三角形,∴MN为△AEF的中位线,∴MNmin=
,且∠MHN=∠HFN=60°,∴△MHN∽△HFN,∴△MHN∽△HFN∽△MEH,在△HMN中,∠MHN=60°,根据三角形中大边对大角,∴要MN最小,只有△HMN是等边三角形,∴∠AMN=60°,∵∠AEF=60°,MN∴MN∥EF,∵△AEF为等边三角形,∴MN为△AEF的中位线,∴MNmin=![]() EF=
EF=![]() ×2=1.
×2=1.

 阅读快车系列答案
阅读快车系列答案