题目内容
【题目】如图形似“w”的函数是由抛物线y1的一部分，其表达式为：y1=
（x2﹣2x﹣3）（x≤3）以及抛物线y2的一部分所构成的，其中曲线y2与曲线y1关于直线x=3对称，A、B是曲线y1与x轴两交点（A在B的左边），C是曲线y1与y轴交点．
（1）求A，B，C三点的坐标和曲线y2的表达式；
（2）我们把其中一条对角线被另一条对角线垂直且平分的四边形称为筝形．过点C作x轴的平行线与曲线y1交于另一个点D，连接AD．试问：在曲线y2上是否存在一点M，使得四边形ACDM为筝形？若存在，计算出点M的横坐标，若不存在，说明理由．
【答案】（1）A（﹣1，0），B（3，0），C（0，﹣
）．y2=
（x2﹣10x+21）（x≥3）；（2）存在，xM=
．
【解析】
试题分析：（1）根据y1的解析式求出A,B,C三点坐标，再根据曲线y2与曲线y1关于直线x=3对称，求出y2与x轴的交点坐标，最后由待定系数法求出函数y2解析式即可；（2）先确定出点P的坐标和CP的解析式，然后与y2解析式形成方程，从而求出M点的横坐标．
试题解析：（1）根据y1的解析式求出A,B,C三点坐标，在y1=
（x2﹣2x﹣3）中，令y1=0，则有
（x2﹣2x﹣3）=0，解得x=﹣1或x=3，∴A（﹣1，0），B（3，0），∵C为曲线y1与y轴的交点，∴C（0，﹣
）．又∵曲线y1与曲线y2关于直线x=3对称，∴曲线y2与x轴两交点坐标分别为（3，0）与（7，0），因为两抛物线形状相同，所以a值相同，∴y2=（x﹣3）（x﹣7）=（x2﹣10x+21）（x≥3）；（2）如图，
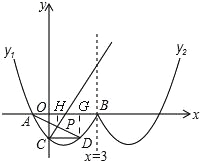
过点D作DG⊥x轴，过点P作PH⊥x轴，∴PH=
DG=
，AH=
AG=
，∴OH=AH﹣AO=，∴P（，
），∴设线段AD的垂直平分线CP的解析式为y=kx+m，∵点C（0，﹣
），∴
，∴
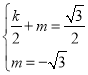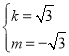，∴CP的解析式为y=x﹣，若直线CP与曲线y2=
（x2﹣10x+21）（x≥3）有交点，则（x2﹣10x+21）=x﹣，化简得：
，解得：x=
或x=
（舍去，∵x＜3）．∴xM=．
