题目内容
【题目】某市人民广场上要建一个圆形的喷水池，并在水池中央垂直安装一个柱子OP，柱子顶端P处装上喷头，由P处向外喷出的水流（在各个方向上）沿形状相同的抛物线路径落下（如图所示）．若已知OP=3米，喷出的水流的最高点A距水平面的高度是4米，离柱子OP的距离为1米．
（1）求这条抛物线的解析式；
（2）若不计其它因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外．
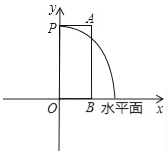
【答案】（1）y=﹣（x﹣1）2+4；（2）3．
【解析】试题分析: （1）根据题意可设解析式为顶点式形式，由A、P两点坐标求解析式；
（2）求水池半径即时求当y=0时x的值．
试题解析:
解：（1）设这条抛物线解析式为y=a（x+m）2+k
由题意知：顶点A为（1，4），P为（0，3）
∴4=k，3=a（0﹣1）2+4，a=﹣1．
所以这条抛物线的解析式为y=﹣（x﹣1）2+4．
（2）令y=0，则0=﹣（x﹣1）2+4，
解得x1=3，x2=﹣1
所以若不计其它因素，水池的半径至少3米，才能使喷出的水流不至于落在池外．
点睛: 本题考查二次函数的性质、配方法等知识，解题的关键是学会构建二次函数解决实际问题，属于中考常考题型．
练习册系列答案
相关题目
