题目内容
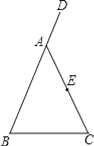
【题目】如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
【答案】(1)作图见解析;(2)AF∥BC且AF=BC,理由见解析.
【解析】试题分析:(1)根据题意画出图形即可;
(2)根据等腰三角形的性质,可得两底角相等,根据三角形的外角的性质,可得∠DAC=∠ABC+∠C,根据内错角相等,可得两直线平行,根据ASA,可得两个三角形全等,根据全等三角形的性质,可得证明结论.
试题解析:(1)如图:
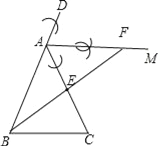
(2)AF∥BC且AF=BC,理由如下:
∵AB=AC,∴∠ABC=∠C,
∵∠DAC=∠ABC+∠C,∴∠DAC=2∠C,
由作图可知∠DAC=2∠FAC,∴∠C=∠FAC,∴AF∥BC;
∵E是AC的中点,∴AE=CE,
在△AEF和△CEB中, 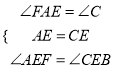 ,∴△AEF≌△CEB (ASA),
,∴△AEF≌△CEB (ASA),
∴AF=BC.

练习册系列答案
相关题目