Question

【题目】如图，△ABC中，AB=AC=10，BC= ，以AB为直径的⊙O分别交BC、AC于点D、E.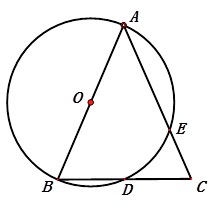

（1）求AE；
（2）过D作DF⊥AC于F，请画出图形，说明DF是否是⊙O的切线，并写出理由；
（3）延长FD，交AB的延长线于G，请画出图形，并求BG.

Answer 1

【答案】
（1）

解：方法一：连结AD、DE

易证BD=CD= ,

△DCE∽△ABC（或△DCA∽△ECB）

∴CE:CB=CB:CA

∴CE=4，AE=6

方法二：BE⊥AC

∴

∴

∴AE=6

方法三： 易证A D=

∵BC×AD=AC×BE,

∴BE=8

∴AE=6

（2）

解：DF是⊙O的切线，理由如下：

方法一：BD=CD,OB=OA,

∴OD∥AC

∴DF⊥AC

∴DF是⊙O的切线

方法二：∠ODB=∠B=∠C,

∴OD∥AC

∴DF⊥AC

∴DF是⊙O的切线

（3）

解：方法一： DE=BD=

∠GBD=∠DEA，∠ GDB=∠FDC=∠DAE

∴ △GBD∽△DEA

∴GB:DE=BD:AE BG=

方法二：BE∥GF,

∴ △ABE∽△AGF

∴AB:BG=AE:EF

BG=

【解析】此题考查圆的切线的判定及性质、相似三角形的判定及性质，准确作出辅助线，分析题中图形之间的关系，此题方法较多，理解、分析透彻图形之间、线段之间的关系是解题关键.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识，掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．