题目内容
【题目】如图,![]() 中
中![]() ,其中
,其中![]() ;
;
(1)求线段![]() 的长(用
的长(用![]() 和
和![]() 的代数式表示);
的代数式表示);
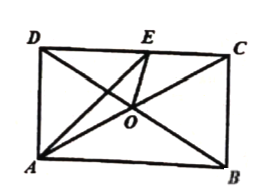
(2)如图1,若![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,点
上,点![]() 到
到![]() 和BC的距离相等,
和BC的距离相等,![]() ,连接
,连接![]() ,求
,求![]() 的长;
的长;
(3)如图2,若![]() 为
为![]() 的中点,
的中点,![]() ,点
,点![]() 分别在线段
分别在线段![]() 上,且
上,且![]() ,连接
,连接![]() ,
,![]() 和
和![]() ,求EF的值;
,求EF的值;

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理计算即可;
(2)过F作FM⊥AC于M,FN⊥BC于N,证明四边形FNCM为正方形,利用FN∥AC,得到![]() ,解出正方形的边长,运用勾股定理可求出DF的长;
,解出正方形的边长,运用勾股定理可求出DF的长;
(3)过F作FG⊥AC于点G,根据已知条件证明△ECD≌△DGF,得到条件证明△EDF为等腰直角三角形,再根据等腰直角三角形的性质可求得结果.
解:(1)根据勾股定理,∵BC=a,AC=b,∠ACB=90°,
∴AB=![]() ;
;
(2)由题意可得:BC=6,AC=8,
∴AB=![]() ,
,
过F作FM⊥AC于M,FN⊥BC于N,
∵F到AC和BC距离相等,
可得四边形FNCM为正方形,
设CM=CN=FN=FM=x,
∵FN⊥BC,AC⊥BC,
∴FN∥AC,
∴![]() ,即
,即![]() ,
,
解得:x=![]() ,
,
∴AM=8-x=![]() ,
,
∵AF=AD,
∴AF=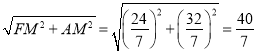 =AD,
=AD,
∴DM=AD-AM=![]() ,
,
∴DF= ;
;

(3)由题意可得:BC=6,AC=8,
∴AB=![]() ,
,
∵F为AB中点,
∴AF=BF=5,
过F作FG⊥AC于点G,
∴FG=![]() BC=3,
BC=3,
∴AG=![]() ,
,
∵BE=BF,AF=AD,
∴BE=5,CE=1,AD=5,CD=3,DG=AD-AG=1,
在△ECD和△DGF中,
 ,
,
∴△ECD≌△DGF(SAS),
∴ED=FD,∠EDC=∠DFG,
∵∠DFG+∠FDG=90°,
∴∠EDC+∠FDG=90°,
∴∠EDF=90°,
∴△EDF为等腰直角三角形,
∵EC=1,CD=3,
∴ED=![]() =FD,
=FD,
∴EF=![]() .
.


练习册系列答案
相关题目