Question

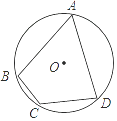
【题目】如图，四边形ABCD内接于⊙O，∠BAD=90°， = ，过点C作CE⊥AD，垂足为E，若AE=3，DE= ，求∠ABC的度数．

Answer 1

【答案】解：作BF⊥CE于F，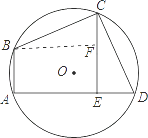

∵∠BCF+∠DCE=90°，∠D+∠DCE=90°，
∴∠BCF=∠D．
又BC=CD，
∴Rt△BCF≌Rt△CDE．
∴BF=CE．
又∵∠BFE=∠AEF=∠A=90°，
∴四边形ABFE是矩形．
∴BF=AE．
∴AE=CE=3，
在Rt△CDE中
∵
∴∠D=60°
∵∠ABC+∠D=180°
∴∠ABC=120°．
【解析】由弧BC=弧CD ，可得弦BC=CD ,需作BF⊥CE于F，构造全等三角形，Rt△BCF≌Rt△CDE，由三角函数求出tan D，由∠BCF=∠D，再利用圆内接四边形性质，求出∠ABC的度数.