题目内容
【题目】课外兴趣小组活动时,老师提出了如下问题:
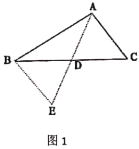
(1)如图1,![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将
的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() 、
、![]() 集中在
集中在![]() 中,利用三角形的三边关系可得
中,利用三角形的三边关系可得![]() ,则
,则![]() ;
;
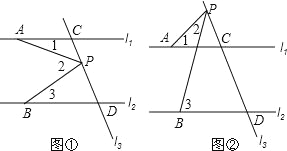
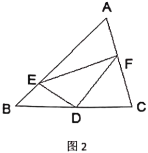
(2)问题解决:受到(1)的启发,请你证明下面命题:如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
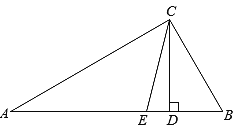
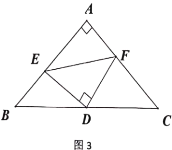
②如图3,若![]() ,探索线段
,探索线段![]() 、
、![]() 、
、![]() 之间的等量关系,并加以证明.
之间的等量关系,并加以证明.
【答案】(2)①见解析;②![]()
【解析】
(2)①可按阅读理解中的方法构造全等,把CF和BE转移到一个三角形中求解;
②由(1)中的全等得到∠C=∠CBG.∵∠ABC+∠C=90°,∴∠EBG=90°,可得三边之间存在勾股定理关系.
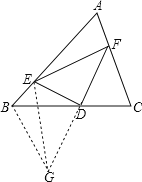
解:(2)①把△CFD绕点D逆时针旋转180°得到△BGD,
![]()
∴CF=BG,DF=DG,
∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
②若∠A=90°,则∠EBC+∠FCB=90°,
由(1)知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,![]()
![]()
∴![]() .
.
![]()
![]() 、
、![]() 、
、![]() 之间的等量关系为
之间的等量关系为![]()

练习册系列答案
相关题目