题目内容
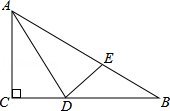
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
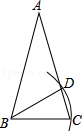

| A.30° | B.45° | C.60° | D.90° |
B.
试题分析:根据等腰三角形两底角相等求出∠ABC=∠ACB,再求出∠CBD,然后根据∠ABD=∠ABC﹣∠CBD计算即可得解:
∵AB=AC,∠A=30°,∴∠ABC=∠ACB=
 (180°﹣∠A)=
(180°﹣∠A)= (180°﹣30°)=75°.
(180°﹣30°)=75°.∵以B为圆心,BC的长为半径圆弧,交AC于点D,∴BC=BD.
∴∠CBD=180°﹣2∠ACB=180°﹣2×75°="30°." ∴∠ABD=∠ABC﹣∠CBD=75°﹣30°=45°.
故选B.

练习册系列答案
相关题目
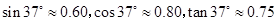 ).
).
 ,则称这个三角形为勾股三角形.
,则称这个三角形为勾股三角形. ,AC=1+
,AC=1+ ,BC=2,⊙O的直径BE交AC于点D.
,BC=2,⊙O的直径BE交AC于点D.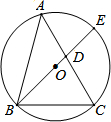



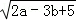 +(2a+3b﹣13)2=0,则此等腰三角形的周长为( )
+(2a+3b﹣13)2=0,则此等腰三角形的周长为( )