��Ŀ����
ѧϰ�˹��ɶ������涨��������֪������һ���������У�������ߵ�ƽ���͵��ڵ����ߵ�ƽ������ô���������Ϊֱ�������Σ����Ƶأ����Ƕ��壺��������������Σ����������ڽǵĶ����ֱ�Ϊx�㡢y���z�㣬������ ��������������Ϊ���������Σ�
������������������������
��1�����ݡ����������Ρ��Ķ��壬����ֱ���ж����⣺��ֱ���������ǹ��������Ρ���������Ǽ����⣿
��2����֪ijһ���������ε������ڽǵĶ�����С��������Ϊx�㡢y���z�㣬��xy=2160����x+y��ֵ��
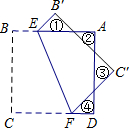
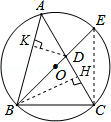
��3����ͼ����ABC�ڽ��ڡ�O��AB= ��AC=1+
��AC=1+ ��BC=2����O��ֱ��BE��AC�ڵ�D��
��BC=2����O��ֱ��BE��AC�ڵ�D��
����֤����ABC�ǹ��������Σ�
����DE�ij���
 ������������������������
��������������Ϊ���������Σ���1�����ݡ����������Ρ��Ķ��壬����ֱ���ж����⣺��ֱ���������ǹ��������Ρ���������Ǽ����⣿
��2����֪ijһ���������ε������ڽǵĶ�����С��������Ϊx�㡢y���z�㣬��xy=2160����x+y��ֵ��
��3����ͼ����ABC�ڽ��ڡ�O��AB=
 ��AC=1+
��AC=1+ ��BC=2����O��ֱ��BE��AC�ڵ�D��
��BC=2����O��ֱ��BE��AC�ڵ�D������֤����ABC�ǹ��������Σ�
����DE�ij���

(1) �����⣻(2)102; (3) ��֤���������� .
.
 .
.���������(1��ֱ�Ӹ��ݡ����������Ρ��Ķ��壬�жϵó����ɣ�
��2��������֪�����ó���������ϵ��ɷ����飬�������x+y��ֵ��
��3���ٹ�B��BH��AC��H����AH=x�����ù��ɶ������ȵó�AH=BH=
 ��HC=1�������ó���A=45�㣬��C=60�㣬��B=75�㣬���ɵó��𰸣�
��HC=1�������ó���A=45�㣬��C=60�㣬��B=75�㣬���ɵó��𰸣��ڹ�D��DK��AB��K����KD=h�����ȵó�h+
 h=
h= �������ó�h��ֵ�����BD�������ó�DE�ij���
�������ó�h��ֵ�����BD�������ó�DE�ij��������������1�������⣻
��2��������ɵã�
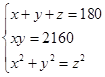 ��
����ã�x+y=102��
��3����֤������B��BH��AC��H����AH=x��
Rt��ABH��BH=
 ��
��Rt��CBH����
 ��2+��1+
��2+��1+ ��x��2=4��
��x��2=4����ã�x=
 ��
�����ԣ�AH=BH=
 ��HC=1��
��HC=1�����A=��ABH=45�㣬
��tan��HBC=
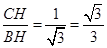 ��
�����HBC=30�㣬
���BCH=60�㣬��B=75�㣬
��452+602=752
���ABC�ǹ��������Σ�
������CE��
�ߡ�A=45�㣬
���BEC=��BAC=45�㣬
�֡�BE��ֱ����
���BCE=90�㣬
��BC=CE=2��
��D��DK��AB��K����KD=h��
�ߡ�EBC=45�㣬��ABC=75�㣬
���ABE=30�㣬
��
 ��AK=h��
��AK=h����h+
 h=
h= ��
����ã�h=
 ��
����BD=2KD=2h=
 ��
����DE=BE��BD=
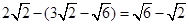
����:1.Բ���ۺ��⣻2.���ɶ�����

��ϰ��ϵ�д�
 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����Ŀ
 .
.
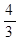 ,����AB�ij�.
,����AB�ij�.