题目内容
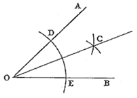
【题目】如图,点O为直线AB上一点,过点O作射线OC,将一直角三角板按图中所示的方式摆放(∠MON=900)
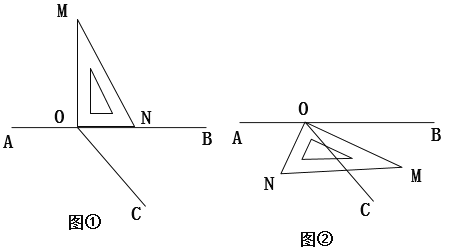
探究一:将图①中的三角板绕点0顺时针方向旋转一定的角度得到图②,使边OM恰好平分∠BOC。若∠BOC=500,ON是否平分∠A0C? 请说明理由;
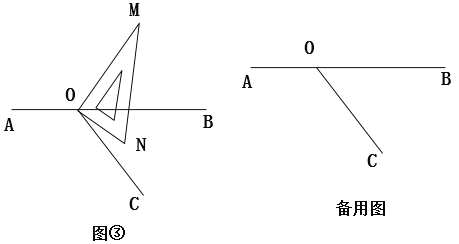
探究二:将图①中的三角板绕点O时针旋转一定的角度得到图③,
(1)使边ON在∠BOC的内部,如果∠BOC=600,则∠BOM与∠CON之间存在怎样的数量关系?请说明理由。
(2)使边ON在∠BOC的内部,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
【答案】探究一、ON平分∠AOC,理由见解析;探究二、(1)∠BOM-∠CON=300 ,理由见解析;(2)∠BOM=∠NOC+30°, 理由见解析.
【解析】
探究一:角平分线的定义可知∠BOM=∠MOC,由∠NOM=90°,可知∠BOM+∠AON=90°,∠MOC+∠NOC=90°,根据等角的余角相等可知∠AON=∠NOC;
探究二:(1)根据题意可知∠NOC+∠NOB=60°,∠BOM+∠NOB=90°,由∠BOM=90°∠NOB、∠BON=60°∠NOC可得到∠BOM=∠NOC+30°.
(2)根据∠CON+∠NOB=60°、∠BOM+∠NOB=90°可得∠BOM=∠NOC+30°.
解:探究一、ON平分∠AOC,
理由如下:∵OM平分∠BOC,且∠BOC=50°
∴∠BOM=∠COM=25°
∵∠MON=90°
∴∠CON=90°-25°=65°
∵∠AON=180°-90°-25°=65°
∴∠CON=∠AON
∴ON平分∠AOC
探究二、(1)∠BOM-∠CON=30°
∵∠MON=90°
∴∠BON=90°-∠BOM
∵∠BOC=60°
∴∠BON=60°-∠CON
∴90°-∠BOM=60°-∠CON
即:∠BOM-∠CON=300 .
(2)∠BOM=∠NOC+30°.理由如下:
∵∠CON+∠NOB=60°,∠BOM+∠NOB=90°
∴∠BOM=∠NOC+30°.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
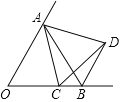
一线名师口算应用题天天练一本全系列答案【题目】如图,△ABC中,AB=AC=2,∠B=30°,点D在BC上,过点D作DE⊥BC,交BA或其延长线于点E,过点E作EF⊥BA交AC或其延长线于点F,连接DF.若DF⊥AC,则BD=_____.