题目内容
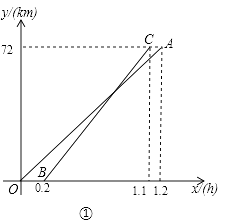
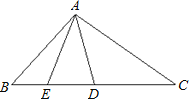
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
【答案】A
【解析】先判断出OA=OB,∠OAB=∠ABO,分两种情况判断出△AOC≌△ABD,进而判断出∠ABD=∠AOB=60°,即可得出结论.
∵∠AOB=60°,OA=OB,
∴△OAB是等边三角形,
∴OA=AB,∠OAB=∠ABO=60°
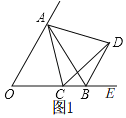
①当点C在线段OB上时,如图1,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD,
在△AOC和△ABD中,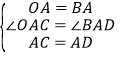 ,
,
∴△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠ABE=180°﹣∠ABO﹣∠ABD=60°=∠AOB,
∴BD∥OA;
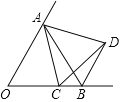
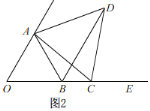
②当点C在OB的延长线上时,如图2,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
∴∠OAC=∠BAD,
在△AOC和△ABD中,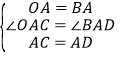 ,
,
∴△AOC≌△ABD,
∴∠ABD=∠AOC=60°,
∴∠ABE=180°﹣∠ABO﹣∠ABD=60°=∠AOB,
∴BD∥OA,
故选A.

练习册系列答案
相关题目
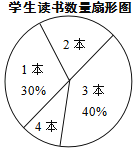
【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?