题目内容
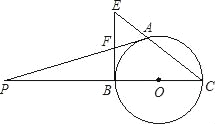
【题目】已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P.
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
【答案】(1)证明见解析(2)3.6
【解析】分析:(1)要想证PA是⊙O的切线,只要连接OA,求证∠OAP=90°即可;
(2)先由切线长定理可知BF=AF,再在Rt△BCE中根据勾股定理求出CE,最后由切割线定理求出AE的长.
详解:(1)证明:连接AB,OA,OF;
∵F是BE的中点,
∴FE=BF.
∵OB=OC,
∴OF∥EC.
∴∠C=∠POF.
∴∠AOF=∠CAO.
∵∠C=∠CAO,
∴∠POF=∠AOF.
∵BO=AO,OF=OF,
∴△OAF≌OBF,
∴∠OAP=∠EBC=90°.
∴PA是⊙O的切线.
(2)解:∵BE是⊙O的切线,PA是⊙O的切线,
∴BF=AF=3,
∴BE=6.
∵BC=8,∠CBE=90°,
∴CE=10.
∵BE是⊙O的切线,
∴EB2=AEEC.
∴AE=3.6.

练习册系列答案
相关题目