��Ŀ����
����Ŀ��ij��˾����һ�ֲ�Ʒ��Ϊ��֤������ÿ�����ڲ�����Ʒ����������100���ڣ������ɱ�C����Ʒ����x�Ķ��κ������������������
������Ʒ������x/���� | 10 | 20 | 30 |
�����ɱ���C/Ԫ�� | 120 | 180 | 260 |
��Ʒ�����ۼ۸�λ��Ԫ��ΪP=35��![]() x��ÿ�����ڵIJ�������=Px��C��
x��ÿ�����ڵIJ�������=Px��C��
��1��ֱ��д�������ɱ�C����Ʒ����x�ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ��
��2���ù�˾ÿ�����ڲ������ټ���Ʒʱ������ﵽ220Ԫ��
��3����ù�˾ÿ�����ڵIJ�����������ֵ��
���𰸡�(1)C=![]() +3x+80��(2)�ù�˾ÿ�����ڲ���10����Ʒʱ������ﵽ220Ԫ��(3)��ÿ�����ڲ���80����Ʒʱ����������������ֵΪ1200 Ԫ��
+3x+80��(2)�ù�˾ÿ�����ڲ���10����Ʒʱ������ﵽ220Ԫ��(3)��ÿ�����ڲ���80����Ʒʱ����������������ֵΪ1200 Ԫ��
��������
�����������1�������������C��x�ĺ�����ϵʽ��Ȼ����ݱ����е����ݼ��ɽ���⣻
��2��������������г���Ӧ�ķ��̣��Ӷ����Խ���⣻
��3������������Եõ����������ۼ۸�Ĺ�ϵʽ��Ȼ��Ϊ����ʽ���ɽ���⣮
�����������1����C=![]() +bx+c��
+bx+c��
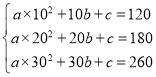 ��
��
��ã�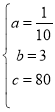 ��
��
�������ɱ�C����Ʒ����x�ĺ�����ϵʽ�ǣ�C=![]() +3x+80��
+3x+80��
��2�������⣬�ã�35��![]() x��x����
x��x����![]() +3x+80��=220��
+3x+80��=220��
��ã�![]() =10��
=10��![]() =150��
=150��
��ÿ�����ڲ�����Ʒ����������100���ڣ�
��x=10��
���ù�˾ÿ�����ڲ���10����Ʒʱ������ﵽ220Ԫ��
��3����ÿ�����ڵIJ�������ΪyԪ��
��y=��35��![]() x��x����
x��x����![]() +3x+80��=
+3x+80��=![]() +32x��80=
+32x��80=![]() ��
��
����x=80ʱ�����������ֵ����ʱy=1200��
����ÿ�����ڲ���80����Ʒʱ����������������ֵΪ1200 Ԫ��

����Ŀ��10��ͬѧ�ֳɼס������ӽ�������������������ߣ���λ��cm�����±���ʾ��
��Ա1 | ��Ա2 | ��Ա3 | ��Ա4 | ��Ա5 | |
�� | 177 | 176 | 175 | 172 | 175 |
�Ҷ� | 170 | 175 | 173 | 174 | 183 |
�����Ӷ�Ա���ߵ�ƽ��������Ϊ![]() ����
���� ![]() �������ߵķ�������Ϊ
�������ߵķ�������Ϊ![]() �������й�ϵ����ȫ��ȷ������ ��
�������й�ϵ����ȫ��ȷ������ ��
A. ![]() ��=
��=![]() ����
���� ![]() B.
B. ![]() ��=
��=![]() ����
���� ![]()
C. ![]() ��>
��>![]() ����
���� ![]() D.
D. ![]() ��<
��<![]() ����
���� ![]()