题目内容
【题目】如图①点A,B,C,D在同一直线上,AB=CD,作CE⊥AD,BF⊥AD,且AE=DF. 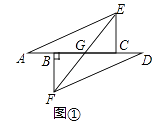
(1)证明:EF平分线段BC;
(2)若△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由. 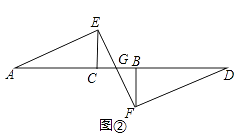
【答案】
(1)证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB+BC=BC+CD,即AC=DB,
在Rt△ACE和Rt△DBF中,
![]() ,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
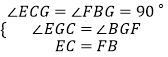 ,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC;
(2)(1)中结论成立,理由为:
证明:∵CE⊥AD,BF⊥AD,
∴∠ACE=∠DBF=90°,
∵AB=CD,
∴AB﹣BC=CD﹣BC,即AC=DB,
在Rt△ACE和Rt△DBF中,
![]() ,
,
∴Rt△ACE≌Rt△DBF(HL),
∴CE=FB,
在△CEG和△BFG中,
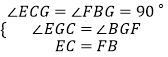 ,
,
∴△CEG≌△BFG(AAS),
∴CG=BG,即EF平分线段BC.
【解析】(1)由AB=CD,利用等式的性质得到AC=BD,再由AE=DF,利用HL得到直角三角形ACE与直角三角形DBF全等,利用全等三角形对应边相等得到EC=BF,再利用AAS得到三角形ECG与三角形FBG全等,利用全等三角形对应边相等得到BG=CG,即可得证;(2)(1)中的结论成立,理由为:由AC=DB,利用等式的性质得到AC=BD,再由AE=DF,利用HL得到直角三角形ACE与直角三角形DBF全等,利用全等三角形对应边相等得到EC=BF,再利用AAS得到三角形ECG与三角形FBG全等,利用全等三角形对应边相等得到BG=CG,即可得证.
【考点精析】通过灵活运用平移的性质,掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等即可以解答此题.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案【题目】某公司产销一种产品,为保证质量,每个周期产销商品件数控制在100以内,产销成本C是商品件数x的二次函数,调查数据如表:
产销商品件数(x/件) | 10 | 20 | 30 |
产销成本(C/元) | 120 | 180 | 260 |
商品的销售价格(单位:元)为P=35﹣![]() x(每个周期的产销利润=Px﹣C)
x(每个周期的产销利润=Px﹣C)
(1)直接写出产销成本C与商品件数x的函数关系式(不要求写出自变量的取值范围)
(2)该公司每个周期产销多少件商品时,利润达到220元?
(3)求该公司每个周期的产销利润的最大值.