题目内容
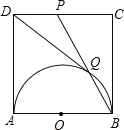
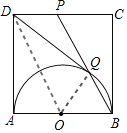
【题目】如图,AB是半圆O的直径,以AB为边在半圆同侧作正方形ABCD,点P是CD中点,BP与半圆交于点Q,连接DQ,设半圆的半径为a.
(1)判断直线DQ与半圆O的位置关系,并说明理由;
(2)求sin∠DQP的值.
【答案】(1)DQ是半圆的切线,理由见解析;(2)![]() .
.
【解析】
(1)连接OQ,OD,得出四边形DOBP是平行四边形,证得△AOD≌△QOD,求得∠OQD=∠OAD=90°,得到OQ⊥DQ,即可得证;(2)求得∠DQP=∠ODQ,OD=![]() =
=![]() ,利用sin∠DQP=sin∠ODQ=
,利用sin∠DQP=sin∠ODQ=![]() 即可求解.
即可求解.
解:(1)DC和半圆O相切
连接OQ,OD,如图
∵DP∥OB,DP=OB
∴四边形DOBP是平行四边形
∴DO∥BP
∴∠AOD=∠OBP,∠DOQ=∠OQB
∵OB=OQ
∴∠OBP=∠OQB
∴∠AOD=∠QOD
∴△AOD≌△QOD(SAS)
∴∠OQD=∠OAD=90°
∴OQ⊥DQ即DQ是半圆的切线
(2)由①可知,DO∥BP
∴∠DQP=∠ODQ
∵DQ=AD=2a,OQ=a
∴∠DQP=∠ODQ
∵DQ=AD=2a,OQ=a
∴OD=![]() =
=![]()
∴sin∠DQP=sin∠ODQ=![]()

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目