��Ŀ����
����Ŀ���������
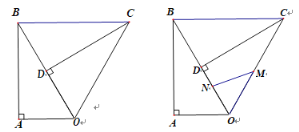
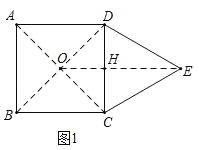
��1����ͼ1��������ABCD�ĶԽ��߽��ڵ�O����CDE�DZ߳�Ϊ6�ĵȱ������Σ���O��E֮��ľ���Ϊ ��
����̽��
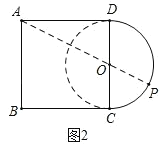
��2����ͼ2���ڱ߳�Ϊ6��������ABCD�У���CDΪֱ������ԲO����PΪ��CD��һ���㣬��A��P֮��������룻
������
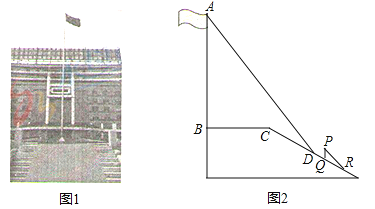
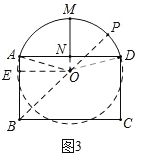
��3��Ҥ������ʡ�±�ũ�����Ҫ������Ҥ�����ݸ���һ�������ķ羰�ߣ�����ΪҤ���������ļ���Լ����е�������֮�⣬�����ж�ů��������Ȼ�ŵ��ס�Ӱ�ũ���һ�Լ����μ��п���˫��̥С����С�����ֵܣ������Լҵ�Ҥ��(��ͼ3��ʾ)���Ŵ����ɾ���ABCD������AMD��ɣ�AB=2m��BC=3.2m������MN=1.2m(NΪAD���е㣬MN��AD)��С��˵���Ž�B���Ŵ����λ�AD����������B��M֮��ľ��룮С��˵�ⲻ�����ľ��룬����Ϊ˭��˵����ȷ����ͨ����������Ž�B���Ŵ����λ�AD�������룮

���𰸡���1��![]() ����2��
����2��![]() ����2��С����˵����ȷ�����ɼ�������
����2��С����˵����ȷ�����ɼ�������![]() ��
��
��������
��1������AC��BD����OE��ֱƽ��DC�ɵ�DH������֪OH��HE������Ӽ��ɣ�
��2����ȫ��O������AO���ӳ�����O�Ұ���ڵ�P�����ʱA��P֮��ľ��������Rt��AOD�У��ɹ��ɶ����ɵ�AO��������AP����
��3��С����˵����ȷ����ȫ���λ�AD���ڵ���O������ON��OA��OD������O��OE��AB�ڵ�E������BO���ӳ�����O�϶��ڵ�P�����ʱB��P֮��ľ��뼴Ϊ�Ž�B���Ŵ����λ�AD�������룬��Rt��ANO�У���AO=r���ɹ��ɶ��������r����Rt��OEB�У��ɹ��ɶ����ɵ�BO������֪BP��.
�⣺��1����ͼ1������AC��BD���Խ��߽���ΪO������OE��CD��H����OD=OC��
�ߡ�DCEΪ�ȱ������Σ�
��ED=EC��
��OD=OC
��OE��ֱƽ��DC��
��DH![]() DC=3��
DC=3��
���ı���ABCDΪ�����Σ�
���OHDΪ����ֱ�������Σ�
��OH=DH=3��
��Rt��DHE��
HE![]() DH=3
DH=3![]() ��
��
��OE=HE+OH=3![]() 3��
3��
��2����ͼ2����ȫ��O������AO���ӳ�����O�Ұ���ڵ�P�����ʱA��P֮��ľ������
��Rt��AOD��AD=6��DO=3��
��AO![]() 3
3![]() ��
��
![]()
��AP=AO+OP=3![]() 3��
3��
��3��С����˵����ȷ���������£�
��ͼ3����ȫ���λ�AD���ڵ���O������ON��OA��OD������O��OE��AB�ڵ�E������BO���ӳ�����O�϶��ڵ�P�����ʱB��P֮��ľ��뼴Ϊ�Ž�B���Ŵ����λ�AD�������룬
������֪����NΪAD���е㣬![]() ��
��
��AN![]() AD=1.6��ON��AD��
AD=1.6��ON��AD��
��Rt��ANO��
��AO=r����ON=r��1.2��
��AN2+ON2=AO2��
��1.62+(r��1.2)2=r2��
��ã�r![]() ��
��
��AE=ON![]() 1.2
1.2![]() ��
��
��Rt��OEB��OE=AN=1.6��BE=AB��AE![]() ��
��
��BO![]() ��
��
��BP=BO+PO![]() ��
��
���Ž�B���Ŵ����λ�AD��������Ϊ![]() ��
��