题目内容
【题目】学习了正多边形之后,小马同学发现利用对称、旋转等方法可以计算等分正多边形面积的方案.
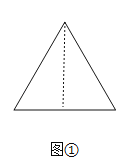
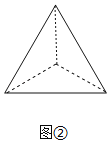
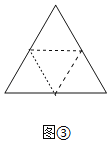
(1)请聪明的你将下面图①、图②、图③的等边三角形分别割成2个、3个、4个全等三角形;
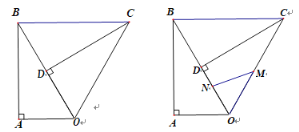
(2)如图④,等边△ABC边长AB=4,点O为它的外心,点M、N分别为边AB、BC上的动点(不与端点重合),且∠MON=120°,若四边形BMON的面积为s,它的周长记为l,求![]() 最小值;
最小值;
(3)如图⑤,等边△ABC的边长AB=4,点P为边CA延长线上一点,点Q为边AB延长线上一点,点D为BC边中点,且∠PDQ=120°,若PA=x,请用含x的代数式表示△BDQ的面积S△BDQ.

【答案】(1)详见解析;(2)2+2![]() ;(3)S△BDQ
;(3)S△BDQ![]() x+
x+![]() .
.
【解析】
(1)根据要求利用全等三角形的判定和性质画出图形即可.
(2)如图④中,作OE⊥AB于E,OF⊥BC于F,连接OB.证明△OEM≌△OFN(ASA),推出EM=FN,ON=OM,S△EOM=S△NOF,推出S四边形BMON=S四边形BEOF=定值,证明Rt△OBE≌Rt△OBF(HL),推出BM+BN=BE+EM+BF﹣FN=2BE=定值,推出欲求![]() 最小值,只要求出l的最小值,因为l=BM+BN+ON+OM=定值+ON+OM所以欲求
最小值,只要求出l的最小值,因为l=BM+BN+ON+OM=定值+ON+OM所以欲求![]() 最小值,只要求出ON+OM的最小值,因为OM=ON,根据垂线段最短可知,当OM与OE重合时,OM定值最小,由此即可解决问题.
最小值,只要求出ON+OM的最小值,因为OM=ON,根据垂线段最短可知,当OM与OE重合时,OM定值最小,由此即可解决问题.
(3)如图⑤中,连接AD,作DE⊥AB于E,DF⊥AC于F.证明△PDF≌△QDE(ASA),即可解决问题.
解:(1)如图1,作一边上的中线可分割成2个全等三角形,
如图2,连接外心和各顶点的线段可分割成3个全等三角形,
如图3,连接各边的中点可分割成4个全等三角形,
(2)如图④中,作OE⊥AB于E,OF⊥BC于F,连接OB.
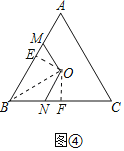
∵△ABC是等边三角形,O是外心,
∴OB平分∠ABC,∠ABC=60°∵OE⊥AB,OF⊥BC,
∴OE=OF,
∵∠OEB=∠OFB=90°,
∴∠EOF+∠EBF=180°,
∴∠EOF=∠NOM=120°,
∴∠EOM=∠FON,
∴△OEM≌△OFN(ASA),
∴EM=FN,ON=OM,S△EOM=S△NOF,
∴S四边形BMON=S四边形BEOF=定值,
∵OB=OB,OE=OF,∠OEB=∠OFB=90°,
∴Rt△OBE≌Rt△OBF(HL),
∴BE=BF,
∴BM+BN=BE+EM+BF﹣FN=2BE=定值,
∴欲求![]() 最小值,只要求出l的最小值,
最小值,只要求出l的最小值,
∵l=BM+BN+ON+OM=定值+ON+OM,
欲求![]() 最小值,只要求出ON+OM的最小值,
最小值,只要求出ON+OM的最小值,
∵OM=ON,根据垂线段最短可知,当OM与OE重合时,OM定值最小,
此时![]() 定值最小,s=
定值最小,s=![]() ×2×
×2×![]() =
=![]() ,l=2+2+
,l=2+2+![]() +
+![]() =4+
=4+![]() ,
,
∴![]() 的最小值=
的最小值=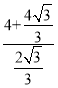 =2+2
=2+2![]() .
.
(3)如图⑤中,连接AD,作DE⊥AB于E,DF⊥AC于F.
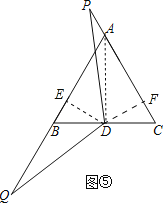
∵△ABC是等边三角形,BD=DC,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠DEA=∠DEQ=∠AFD=90°,
∴∠EAF+∠EDF=180°,
∵∠EAF=60°,
∴∠EDF=∠PDQ=120°,
∴∠PDF=∠QDE,
∴△PDF≌△QDE(ASA),
∴PF=EQ,
在Rt△DCF中,∵DC=2,∠C=60°,∠DFC=90°,
∴CF=![]() CD=1,DF=
CD=1,DF=![]() ,
,
同法可得:BE=1,DE=DF=![]() ,
,
∵AF=AC﹣CF=4﹣1=3,PA=x,
∴PF=EQ=3+x,
∴BQ=EQ﹣BE=2+x,
∴S△BDQ=![]() BQDE=
BQDE=![]() (2+x)×
(2+x)×![]() =
=![]() x+
x+![]() .
.

【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋中并搅匀,让学生进行摸球试验,每次摸出一个球(放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | _____ | _____ | _____ |
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个黑球的概率是______.(结果都保留小数点后两位)
(2)估算袋中白球的个数为________.
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算出两次都摸出白球的概率.