题目内容
如图，⊙C经过原点且与两坐标轴分别交于A、B两点，点A的坐标是（0，4），M是圆上一点，∠BMO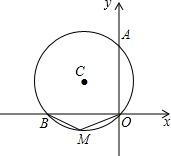
=120°，求⊙C的半径和圆心C的坐标．
=120°，求⊙C的半径和圆心C的坐标．（1）连接AB，AM，则由∠AOB=90°，故AB是直径，
由∠BAM+∠OAM=∠BOM+∠OBM=180°-120°=60°，
得∠BAO=60°，
又AO=4，故cos∠BAO=
，AB=
=8，
从而⊙C的半径为4．
（2）由（1）得，BO=
=4
，
过C作CE⊥OA于E，CF⊥OB于F，
则EC=OF=
BO=
×4
=2
，CF=OE=
OA=2．
故C点坐标为（-2
，2）．
由∠BAM+∠OAM=∠BOM+∠OBM=180°-120°=60°，
得∠BAO=60°，
又AO=4，故cos∠BAO=
| AO |
| AB |
| 4 |
| cos60° |
从而⊙C的半径为4．
（2）由（1）得，BO=
| 82-42 |
| 3 |
过C作CE⊥OA于E，CF⊥OB于F，
则EC=OF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
故C点坐标为（-2
| 3 |
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
