Question

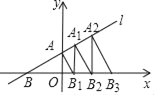
【题目】在平面直角坐标系中，A（3，0）、B（a，2）、C（0，m），D（n，0），且m2+n2=4，若E为CD中点．则AB+BE的最小值为（　　）

A. 3 B. 4 C. 5 D. 2

Answer 1

【答案】B

【解析】

由m2+n2=4，可知CD=2，OE=1，即点E在以点O为圆心，以1为半径的圆上；作点A关于直线y=2的对称点A′，连接A′O，交直线y=2于点B，交圆于点E，由轴对称的性质知此时AB+BE的值最小；然后由勾股定理求出OA′的长，从而可求出EA′的长，即AB+BE的值最小值.

∵m2+n2=4，

∴CD=2，OE=1，

即点E在以点O为圆心，以1为半径的圆上；

作点A关于直线y=2的对称点A′，连接A′O，交直线y=2于点B，交圆于点E，由轴对称的性质知此时AB+BE的值最小；

由勾股定理得，

,

∴EA′=5-1=4，

∴AB+BE=4.

故选B.