题目内容
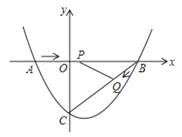
【题目】已知二次函数y=ax2﹣9ax+18a的图象与x轴交于A,B两点(A在B的左侧),图象的顶点为C,直线AC交y轴于点D.
(1)连接BD,若∠BDO=∠CAB,求这个二次函数的表达式;
(2)是否存在以原点O为对称轴的矩形CDEF?若存在,求出这个二次函数的表达式,若不存在,请说明理由.
【答案】(1) y=![]() x2﹣6
x2﹣6![]() x+12
x+12![]() 或y=﹣
或y=﹣![]() x2+6
x2+6![]() x﹣12
x﹣12![]() ;
;
(2)存在,理由见解析.
【解析】
(1)先用含a的代数式表示出顶点坐标,作CM⊥x轴于M,则OM=![]() ,CM=|﹣
,CM=|﹣![]() a|.令y=0求出A、B两点坐标.通过证明△ODA∽△OBD,可求出OD的长,由CM∥OD,求出CM的长,从而可求出a的值;
a|.令y=0求出A、B两点坐标.通过证明△ODA∽△OBD,可求出OD的长,由CM∥OD,求出CM的长,从而可求出a的值;
(2)连接OC,则OC=OD.由平行线的判定与性质可证∠OCD=∠DCM.由∠AON的正弦值求得∠AON=30°,由正切函数求出CM的长,进而可求出a的值.
解:(1)∵y=ax2﹣9ax+18a=a(x﹣![]() )2﹣
)2﹣![]() a,
a,
∴顶点C(![]() ,﹣
,﹣![]() a).
a).
作CM⊥x轴于M,则OM=![]() ,CM=|﹣
,CM=|﹣![]() a|.
a|.
当y=0时,ax2﹣9ax+18a=0,解得x1=3,x2=6,
∴A(3,0),B(6,0).
∵∠BDO=∠CAB,∠CAB=∠DAO,
∴∠DAO=∠BDO.
在△ODA与△OBD中,
![]() ,
,
∴△ODA∽△OBD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴OD=3![]() .
.
∵CM∥OD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CM=![]() ,
,
∴|﹣![]() a|=
a|=![]() ,
,
∴a=±![]() ,
,
∴二次函数的解析式为y=![]() x2﹣6
x2﹣6![]() x+12
x+12![]() 或y=﹣
或y=﹣![]() x2+6
x2+6![]() x﹣12
x﹣12![]() ;
;
(2)存在.连接OC,则OC=OD.
∴∠ODC=∠OCD.
∵CM∥OD,
∴∠ODC=∠DCM,
∴∠OCD=∠DCM.
作AN⊥OC于N,AN=AM=![]() .
.
∵sin∠AON=![]() =
=![]() =
=![]() ,
,
∴∠AON=30°,
∴CM=OMtan30°=![]() ×
×![]() =
=![]() ,
,
∴|﹣![]() a|=
a|=![]() ,
,
∴a=±![]() ,
,
∴二次函数的解析式为y=![]() x2﹣6
x2﹣6![]() x+12
x+12![]() 或y=﹣
或y=﹣![]() x2+6
x2+6![]() x﹣12
x﹣12![]() .
.