题目内容
【题目】国家教育部为支援西部教育发展，计划投入大量资金在西部各省修建A，B两类大型图书馆共10个
若修建A类图书馆1个，B类图书馆2个，共需400万元；若修建A类图书馆2个，B类图书馆1个，共需350万元．
（1）求修建A类和B类图书馆每个各需多少万元？
（2）预计在该计划上A类和B类图书馆年均阅览量分别为60万人次和100万人次若教育部投入A类和B类图书馆的总费用不超过1200万元，且确保这10个图书馆的年均阅览量总和不少于680万人次．如果你是领导，从节约投资费用考虑，请设计出可行的方案．
【答案】（1）修建一个A类图书馆和一个B类图书馆所需的资金分别为100万元和150万元；（2）设计修建A类图书馆8个，B类图书馆2个．
【解析】
（1）设修建一个A类图书馆和一个B类图书馆所需的资金分别为a万元和b万元，然后建立二元一次方程组求解即可；
（2）根据（1）的结论，根据总费用和年均总阅览量建立一个一元一次不等式组，然后根据整数性求解即可得．
（1）设修建一个A类图书馆和一个B类图书馆所需的资金分别为a万元和b万元
依题意得：
解得：
答：修建一个A类图书馆和一个B类图书馆所需的资金分别为100万元和150万元；
（2）设修建A类图书馆x个，则修建B类图书馆为
个
依题意得：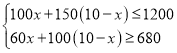
解得
取整数
的取值为6，7，8
要节约投资，且修建一个A类图书馆的费用小于修建一个B类图书馆的费用
类越多越好
从节约投资费用考虑，可行的方案
，
答：设计修建A类图书馆8个，B类图书馆2个．
【题目】如图，AB 是⊙O 的弦，AB=5cm，点 P 是弦 AB 上的一个定点，点 C 是弧 AB 上的一 个动点，连接 CP 并延长，交⊙O 于点 D．
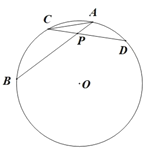
小明根据学习函数的经验，分别对 AC，PC，PD 长度之间的关系进行了探究．
下面是小明的探究过程：
（1）对于点 C 在弧 AB 上的不同位置，画图、测量，得到了线段 AC，PC，PD 的长度的 几组值，如下表：
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | 位置 9 | |
AC/cm | 0 | 0.37 | 1.00 | 1.82 | 2.10 | 3.00 | 3.50 | 3.91 | 5.00 |
PC/cm | 1.00 | 0.81 | 0.69 | 0.75 | 1.26 | 2.11 | 2.50 | 3.00 | 4.00 |
PD/cm | 4.00 | 5.00 | 5.80 | 6.00 | 3.00 | 1.90 | 1.50 | 1.32 | 1.00 |
在 AC，PC，PD 的长度这三个量中，确定＿＿＿的长度是自变量，其他两条线段的长度都是这个自变量的函数；
（2）请你在同一平面直角坐标系 xOy 中， 画（1）中所确定的两个函数的图象；
（3）结合函数图象，解决问题：
①当 PC=PD 时，AC 的长度约为 cm；
②当△APC 为等腰三角形时，PC 的长度约为 cm.
