题目内容
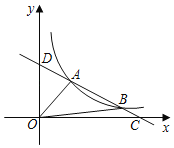
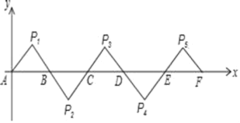
【题目】如图所示,在平面直角坐标系中,A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C,把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,得到的等腰直角三角形的直角顶点P2017的坐标为_____.
【答案】(4033,1)
【解析】
根据等腰直角三角形的性质可找出点P1的坐标,结合旋转的性质即可找出点P2、P3、P4、P5、…、的坐标,根据坐标的变化即可找出变化规律“P2n+1(4n+1,1),P2n+2(4n+3,﹣1)(n为自然数)”,依此规律即可得出结论.
解:∵A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,
∴P1(1,1).
∵把△AP1B绕点B顺时针旋转180°,得到△BP2C1,
∴P2(3,﹣1).
同理可得出:P3(5,1),P4(7,﹣1),P5(9,1),…,
∴P2n+1(4n+1,1),P2n+2(4n+3,﹣1)(n为自然数).
∵2017=2×1008+1,
∴P2017(4033,1).
故答案为:(4033,1)

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目