ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋČįÍžĢŽŌŅÖŠĄũABCÖÐĢŽAB=10cmĢŽAC=8cmĢŽBC=6cmĢŪČįđûĩãPÓÉBģö·ĒŅØBAÏōĩãAÔČËŲÔËķŊĢŽÍŽĘąĩãQÓÉAģö·ĒŅØACÏōĩãCÔČËŲÔËķŊĢŽËüÃĮĩÄËŲķČūųΊ2cm/sĢŪÁŽ―ÓPQĢŽÉčÔËķŊĩÄĘąžäΊtĢĻĩĨÎŧĢšsĢĐĢĻ0ĄÜtĄÜ4ĢĐĢŪ
ĢĻ1ĢĐĩątΊšÎÖĩĘąĢŽPQĄÎBCĢŪ
ĢĻ2ĢĐÉčĄũAQPĩÄÃæŧýΊSĢĻĩĨÎŧĢšcm2ĢĐĢŽĩątΊšÎÖĩĘąĢŽSČĄĩÃŨîīóÖĩĢŽēĒĮóģöŨîīóÖĩĢŪ
ĢĻ3ĢĐĘĮ·ņīæÔÚÄģĘąŋĖtĢŽĘđÏßķÎPQĮĄšÃ°ŅĄũABCĩÄÃæŧýÆ―·ÖĢŋČôīæÔÚĢŽĮóģöīËĘątĩÄÖĩĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĢŪ
Ąūīð°ļĄŋ
ĢĻ1ĢĐ
―âĢšÓÉĖâŌâÖŠĢšBP=2tĢŽAP=10Đ2tĢŽAQ=2tĢŽ
ĄßPQĄÎBCĢŽ
ĄāĄũAPQĄŨĄũABCĢŽ
Ąā ![]() =
= ![]() ĢŽ
ĢŽ
Ąā ![]() =
= ![]() ĢŽ
ĢŽ
t= ![]() ĢŽ
ĢŽ
žīĩątΊ ![]() sĘąĢŽPQĄÎBCĢŧ
sĘąĢŽPQĄÎBCĢŧ
ĢĻ2ĢĐ
―âĢšĄßAB=10cmĢŽAC=8cmĢŽBC=6cmĢŽ
ĄāAB2=AC2+BC2ĢŽ
ĄāĄÏC=90ĄãĢŽ
đýPŨũPDĄÍACÓÚDĢŽ
ÔōPDĄÎBCĢŽ
ĄāĄũAPDĄŨĄũABCĢŽ
Ąā ![]() =
= ![]() ĢŽ
ĢŽ
Ąā ![]() =
= ![]() ĢŽ
ĢŽ
PD= ![]() ĢĻ10Đ2tĢĐĢŽ
ĢĻ10Đ2tĢĐĢŽ
ĄāS= ![]() AQPD=
AQPD= ![]() 2t
2t ![]() ĢĻ10Đ2tĢĐ=Đ
ĢĻ10Đ2tĢĐ=Đ ![]() t2+6t=Đ
t2+6t=Đ ![]() ĢĻtĐ
ĢĻtĐ ![]() ĢĐ2+7.5ĢŽ
ĢĐ2+7.5ĢŽ
ĄßĐ ![]() Ģž0ĢŽŋŠŋÚÏōÏÂĢŽÓÐŨîīóÖĩĢŽ
Ģž0ĢŽŋŠŋÚÏōÏÂĢŽÓÐŨîīóÖĩĢŽ
ĩąt= ![]() ÃëĘąĢŽSĩÄŨîīóÖĩĘĮ7.5cm2ĢŪ
ÃëĘąĢŽSĩÄŨîīóÖĩĘĮ7.5cm2ĢŪ

ĢĻ3ĢĐ
―âĢšžŲÉčīæÔÚÄģĘąŋĖtĢŽĘđÏßķÎPQĮĄšÃ°ŅĄũABCĩÄÃæŧýÆ―·ÖĢŽ
ÔōSĄũAPQ= ![]() SĄũABC
SĄũABC
žīĐ ![]() t2+6t=
t2+6t= ![]() ĄÁ
ĄÁ ![]() ĄÁ8ĄÁ6
ĄÁ8ĄÁ6
t2Đ5t+10=0ĢŽ
ĄßĄũ=52Đ4ĄÁ1ĄÁ10=Đ15Ģž0ĢŽ
ĄāīË·―ģĖÎÞ―âĢŽ
žīēŧīæÔÚÄģĘąŋĖtĢŽĘđÏßķÎPQĮĄšÃ°ŅĄũABCĩÄÃæŧýÆ―·ÖĢŪ
Ąū―âÎöĄŋĢĻ1ĢĐÖĪĄũAPQĄŨĄũABCĢŽÍÆģö ![]() =
= ![]() ĢŽīúČëĩÃģö
ĢŽīúČëĩÃģö ![]() =
= ![]() ĢŽĮóģö·―ģĖĩÄ―âžīŋÉĢĻ2ĢĐĮóģöĄÏC=90ĄãĢŽđýPŨũPDĄÍACÓÚDĢŽÖĪĄũAPDĄŨĄũABCĢŽīúČëĩÃģö·―ģĖ
ĢŽĮóģö·―ģĖĩÄ―âžīŋÉĢĻ2ĢĐĮóģöĄÏC=90ĄãĢŽđýPŨũPDĄÍACÓÚDĢŽÖĪĄũAPDĄŨĄũABCĢŽīúČëĩÃģö·―ģĖ ![]() =
= ![]() ĢŽĮóģöPD=
ĢŽĮóģöPD= ![]() ĢĻ10Đ2tĢĐĢŽļųūÝČý―ĮÐÎĩÄÃæŧýđŦĘ―ĮóģöžīŋÉĢŧĢĻ3ĢĐžŲÉčīæÔÚÄģĘąŋĖtĢŽĘđÏßķÎPQĮĄšÃ°ŅĄũABCĩÄÃæŧýÆ―·ÖĢŽĩÃģö·―ģĖĐ
ĢĻ10Đ2tĢĐĢŽļųūÝČý―ĮÐÎĩÄÃæŧýđŦĘ―ĮóģöžīŋÉĢŧĢĻ3ĢĐžŲÉčīæÔÚÄģĘąŋĖtĢŽĘđÏßķÎPQĮĄšÃ°ŅĄũABCĩÄÃæŧýÆ―·ÖĢŽĩÃģö·―ģĖĐ ![]() t2+6t=
t2+6t= ![]() ĄÁ
ĄÁ ![]() ĄÁ8ĄÁ6ĢŽĮóģöīË·―ģĖÎÞ―âĢŽžīŋÉĩÃģöīð°ļĢŪ
ĄÁ8ĄÁ6ĢŽĮóģöīË·―ģĖÎÞ―âĢŽžīŋÉĩÃģöīð°ļĢŪ
ĄūŋžĩãūŦÎöĄŋ―âīðīËĖâĩÄđØžüÔÚÓÚĀí―âÏāËÆČý―ĮÐÎĩÄÐÔÖĘĩÄÏāđØÖŠĘķĢŽÕÆÎÕķÔÓĶ―ĮÏāĩČĢŽķÔÓĶąßģÉąČĀýĩÄÁ―ļöČý―ĮÐÎ―ÐŨöÏāËÆČý―ĮÐÎĢŽŌÔž°ķÔÏāËÆČý―ĮÐÎĩÄÅÐķĻĩÄĀí―âĢŽÁË―âÏāËÆČý―ĮÐÎĩÄÅÐķĻ·―·Ļ:Á――ĮķÔÓĶÏāĩČĢŽÁ―Čý―ĮÐÎÏāËÆĢĻASAĢĐĢŧÖą―ĮČý―ĮÐÎąŧÐąąßÉÏĩÄļß·ÖģÉĩÄÁ―ļöÖą―ĮČý―ĮÐΚÍÔČý―ĮÐÎÏāËÆĢŧ Á―ąßķÔÓĶģÉąČĀýĮŌžÐ―ĮÏāĩČĢŽÁ―Čý―ĮÐÎÏāËÆĢĻSASĢĐĢŧČýąßķÔÓĶģÉąČĀýĢŽÁ―Čý―ĮÐÎÏāËÆĢĻSSSĢĐĢŪ

ĄūĖâÄŋĄŋČįÍžĢŽPĘĮABËųķÔÏŌABÉÏŌŧķŊĩãĢŽđýĩãPŨũPMĄÍAB―ŧABÓÚĩãMĢŽÁŽ―ÓMBĢŽđýĩãPŨũPNĄÍMBÓÚĩãNĢŪŌŅÖŠAB=6cmĢŽÉčAĄĒPÁ―ĩãžäĩÄūāĀëΊxcmĢŽPĄĒNÁ―ĩãžäĩÄūāĀëΊycmĢŪĢĻĩąĩãPÓëĩãAŧōĩãBÖØšÏĘąĢŽyĩÄÖĩΊ0ĢĐ 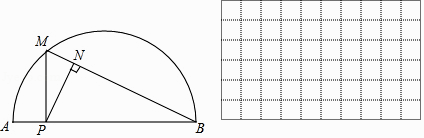
ÐĄķŦļųūÝŅ§Ï°šŊĘýĩÄūŅéĢŽķÔšŊĘýyËæŨÔąäÁŋxĩÄąäŧŊķøąäŧŊĩÄđæÂÉ―øÐÐÁËĖ―ūŋĢŪ
ÏÂÃæĘĮÐĄķŦĩÄĖ―ūŋđýģĖĢŽĮëēđģäÍęÕûĢš
ĢĻ1ĢĐÍĻđýČĄĩãĄĒŧÍžĄĒēâÁŋĢŽĩÃĩ―ÁËxÓëyĩÄžļŨéÖĩĢŽČįÏÂąíĢš
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.0 | 2.3 | 2.1 | 0.9 | 0 |
ĢĻËĩÃũĢšēđČŦąíļņĘąÏāđØĘýÖĩąĢÁôŌŧÎŧÐĄĘýĢĐ
ĢĻ2ĢĐ―ĻÁĒÆ―ÃæÖą―ĮŨøąęÏĩĢŽÃčģöŌÔēđČŦšóĩÄąíÖÐļũķÔķÔÓĶÖĩΊŨøąęĩÄĩãĢŽŧģöļÚŊĘýĩÄÍžÏóĢŪ 
ĢĻ3ĢĐ―ášÏŧģöĩÄšŊĘýÍžÏóĢŽ―âūöÎĘĖâĢšĩąĄũPANΊĩČŅüČý―ĮÐÎĘąĢŽAPĩÄģĪķČԞΊcmĢŪ