题目内容
【题目】在信宜市某“三华李”种植基地有A、B两个品种的树苗出售，已知A种比B种每株多2元，买1株A种树苗和2株B种树苗共需20元．
（1）问A、B两种树苗每株分别是多少元？
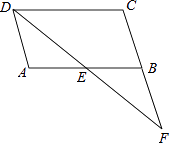
（2）为扩大种植，某农户准备购买A、B两种树苗共360株，且A种树苗数量不少于B种数量的一半，请求出费用最省的购买方案．
【答案】
（1）解：设A种树苗每株x元，B种树苗每株y元，由题意，得
，
解得： 
，
答：A种树苗每株8元，B种树苗每株6元
（2）解：设A种树苗购买a株，则B种树苗购买（360﹣a）株，共需要的费用为W元，由题意，得
，
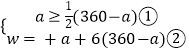由①，得
a≥120．
由②，得
W=2a+2160．
∵k=2＞0，
∴W随a的增大而增大，
∴a=120时，W最小=2400，
∴B种树苗为：360﹣120=240棵．
∴最省的购买方案是：A种树苗购买120棵，B种树苗购买240棵
【解析】（1）设A种树苗每株x元，B种树苗每株y元，根据条件建立方程求出其解即可；（2）设A种树苗购买a株，则B种树苗购买（360﹣a）株，共需要的费用为W元，根据条件建立不等式组，求出其解即可．
【题目】某公司生产的某种商品每件成本为20元，经过市场调研发现，这种商品在未来40天内的日销售量m（件）与时间t（天）的关系如下表：
时间t（天） | 1 | 3 | 5 | 10 | 36 | … |
日销售量m（件） | 94 | 90 | 86 | 76 | 24 | … |
未来40天内，前20天每天的价格y1（元/件）与时间t（天）的函数关系式为y1= 
t+25（1≤t≤20且t为整数），后20天每天的价格y2（元/件）与时间t（天）的函数关系式为y2=﹣ 
t+40（21≤t≤40且t为整数）．
下面我们就来研究销售这种商品的有关问题：
（1）认真分析上表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m（件）与t（天）之间的表达式；
（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？
